Bài học hôm nay, chúng ta sẽ cùng nhau khám phá hai tính chất quan trọng của phép cộng: tính chất giao hoán và tính chất kết hợp. Đây là những kiến thức nền tảng giúp các em học sinh lớp 4 thực hiện các phép tính cộng một cách nhanh chóng và chính xác hơn.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu cho Bài 24. Tính chất giao hoán và kết hợp của phép cộng (tiết 2) trang 68 Vở thực hành Toán 4, giúp các em nắm vững kiến thức và tự tin giải bài tập.
Tính bằng cách thuận tiện. a) 68+ 207 + 3 Tính giá trị của biểu thức (a + b) + c với a = 1 975, b = 1 991 và c = 2 025.
Tính bằng cách thuận tiện.
a) 68+ 207 + 3
b) 25 + 159 + 75
c) 1 + 99 + 340
d) 372 + 290 + 10 + 28
Phương pháp giải:
Khi cộng tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba:
(a + b) + c = a + (b + c)
Lời giải chi tiết:
a) 68 + 207 + 3 = 68 + (207 + 3)
= 68 + 210 = 278
b) 25 + 159 + 75 = (25 + 75) + 159
= 100 + 159 = 259
c) 1 + 99 + 340 = 100 + 340 = 440
d) 372 + 290 + 10 + 28 = (372 + 28) + (290 + 10)
= 400 + 300 = 700
Tính giá trị của biểu thức (a + b) + c với a = 1 975, b = 1 991 và c = 2 025.
Phương pháp giải:
- Thay chữ bằng số vào biểu thức
- Áp dụng tính chất kết hợp để nhóm hai số có tổng là số tròn nghìn với nhau:
(a + b) + c = a + (b + c)
Lời giải chi tiết:
Với a = 19 75, b = 1 991 và c = 2 025 thì:
(a + b) + c = (1 975 + 1 991) + 2 025
= (1 975 + 2 025) + 1 991
= 4 000 + 1 991
= 5 991
Viết số thích hợp vào chỗ chấm.
a) 2 098 + 9 182 = 9 182 + ............
b) 818 + 847 + 222 = 818 + ...........+ 847
c) 198 + 288 + 333 = 333 + 288 + ...........
Phương pháp giải:
Áp dụng tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi
Lời giải chi tiết:
a) 2 098 + 9 182 = 9 182 + 2 098
b) 818 + 847 + 222 = 818 + 222 + 847
c) 198 + 288 + 333 = 333 + 288 + 198
Tính bằng cách thuận tiện.
a) 68+ 207 + 3
b) 25 + 159 + 75
c) 1 + 99 + 340
d) 372 + 290 + 10 + 28
Phương pháp giải:
Khi cộng tổng hai số với số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba:
(a + b) + c = a + (b + c)
Lời giải chi tiết:
a) 68 + 207 + 3 = 68 + (207 + 3)
= 68 + 210 = 278
b) 25 + 159 + 75 = (25 + 75) + 159
= 100 + 159 = 259
c) 1 + 99 + 340 = 100 + 340 = 440
d) 372 + 290 + 10 + 28 = (372 + 28) + (290 + 10)
= 400 + 300 = 700
Tính giá trị của biểu thức (a + b) + c với a = 1 975, b = 1 991 và c = 2 025.
Phương pháp giải:
- Thay chữ bằng số vào biểu thức
- Áp dụng tính chất kết hợp để nhóm hai số có tổng là số tròn nghìn với nhau:
(a + b) + c = a + (b + c)
Lời giải chi tiết:
Với a = 19 75, b = 1 991 và c = 2 025 thì:
(a + b) + c = (1 975 + 1 991) + 2 025
= (1 975 + 2 025) + 1 991
= 4 000 + 1 991
= 5 991
Hoàn thành bảng sau:
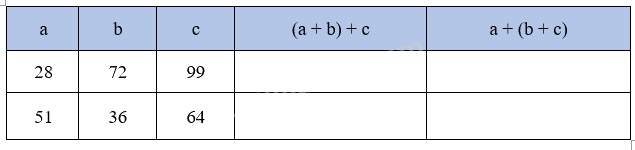
Phương pháp giải:
Thay chữ bằng số vào biểu thức rồi tính giá trị của biểu thức đó
Lời giải chi tiết:

Viết số thích hợp vào chỗ chấm.
a) 2 098 + 9 182 = 9 182 + ............
b) 818 + 847 + 222 = 818 + ...........+ 847
c) 198 + 288 + 333 = 333 + 288 + ...........
Phương pháp giải:
Áp dụng tính chất giao hoán: Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi
Lời giải chi tiết:
a) 2 098 + 9 182 = 9 182 + 2 098
b) 818 + 847 + 222 = 818 + 222 + 847
c) 198 + 288 + 333 = 333 + 288 + 198
Hoàn thành bảng sau:
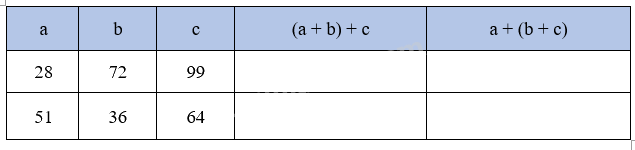
Phương pháp giải:
Thay chữ bằng số vào biểu thức rồi tính giá trị của biểu thức đó
Lời giải chi tiết:

Trong chương trình Toán 4, việc hiểu rõ các tính chất của phép cộng là vô cùng quan trọng. Bài 24 trong Vở thực hành Toán 4 tập trung vào hai tính chất cơ bản: tính chất giao hoán và tính chất kết hợp. Chúng ta sẽ cùng nhau tìm hiểu chi tiết về từng tính chất này, cách áp dụng chúng vào giải toán và thực hành thông qua các bài tập cụ thể.
Tính chất giao hoán của phép cộng khẳng định rằng, khi đổi vị trí các số hạng trong một tổng, giá trị của tổng không thay đổi. Điều này có nghĩa là:
a + b = b + a
Ví dụ:
Tính chất giao hoán giúp chúng ta linh hoạt hơn trong việc sắp xếp các số hạng để thực hiện phép cộng một cách thuận tiện nhất.
Tính chất kết hợp của phép cộng cho phép chúng ta nhóm các số hạng theo nhiều cách khác nhau mà không làm thay đổi giá trị của tổng. Điều này có nghĩa là:
(a + b) + c = a + (b + c)
Ví dụ:
Tính chất kết hợp đặc biệt hữu ích khi chúng ta cần cộng nhiều số hạng với nhau. Nó giúp chúng ta chia nhỏ bài toán thành các bước nhỏ hơn, dễ dàng quản lý và tính toán hơn.
Khi giải các bài toán cộng, chúng ta có thể sử dụng một hoặc cả hai tính chất giao hoán và kết hợp để đơn giản hóa phép tính. Ví dụ:
Tính: 25 + 18 + 32
Chúng ta có thể sử dụng tính chất kết hợp để nhóm 18 và 32 lại với nhau:
25 + (18 + 32) = 25 + 50 = 75
Hoặc chúng ta có thể sử dụng tính chất giao hoán để đổi vị trí các số hạng:
(25 + 32) + 18 = 57 + 18 = 75
Hãy cùng thực hành với một số bài tập sau để củng cố kiến thức về tính chất giao hoán và kết hợp của phép cộng:
Để nắm vững kiến thức về tính chất giao hoán và kết hợp của phép cộng, các em cần:
Hy vọng rằng, với những kiến thức và bài tập thực hành trên, các em học sinh lớp 4 sẽ hiểu rõ hơn về tính chất giao hoán và kết hợp của phép cộng, từ đó học tập môn Toán ngày càng hiệu quả hơn. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức!
| Ví dụ | Giải thích |
|---|---|
| 7 + 9 = 9 + 7 | Tính chất giao hoán: Đổi vị trí các số hạng, tổng không đổi. |
| (4 + 6) + 2 = 4 + (6 + 2) | Tính chất kết hợp: Nhóm các số hạng khác nhau, tổng không đổi. |