Bài học này giúp các em học sinh lớp 4 nắm vững kiến thức về tính chất cơ bản của phân số, đó là việc nhân cả tử số và mẫu số của một phân số với cùng một số khác 0 thì được một phân số bằng phân số đã cho. Bài tập trong Vở thực hành Toán 4 trang 52 sẽ giúp các em rèn luyện kỹ năng áp dụng tính chất này vào giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập, giúp các em tự học hiệu quả và đạt kết quả tốt nhất.
Viết số thích hợp vào chỗ chấm ........
Viết số thích hợp vào chỗ chấm.
$\frac{2}{3} = \frac{{......}}{6}$ ; $\frac{6}{{15}} = \frac{{.......}}{5}$
$\frac{{12}}{{18}} = \frac{2}{{......}}$ ; $\frac{7}{9} = \frac{{......}}{{54}}$
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
$\frac{2}{3} = \frac{4}{6}$ ; $\frac{6}{{15}} = \frac{2}{5}$
$\frac{{12}}{{18}} = \frac{2}{3}$ ; $\frac{7}{9} = \frac{{42}}{{54}}$
Viết số thích hợp vào chỗ chấm.
a) $\frac{8}{{12}} = \frac{{.....}}{3} = \frac{4}{{......}}$
b) $\frac{2}{3} = \frac{6}{{......}} = \frac{{......}}{{18}} = \frac{{.....}}{{45}}$
Cộng các số đã viết ở câu b được kết quả là: .............
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số để tìm các số bị che lấp.
Lời giải chi tiết:

a) Viết số thích hợp vào chỗ chấm.
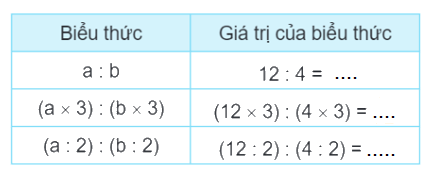
b) >, <, =?
a : b ........ (a x 3) : (b x 3)
a : b ........ (a : 2) : (b : 2)
Phương pháp giải:
a) Tính giá trị biểu thức.
b) Dựa vào nhận xét ở câu a để điền dấu thích hợp.
Lời giải chi tiết:
a)

b)
a : b = (a x 3) : (b x 3)
a : b = (a : 2) : (b : 2)
Viết số thích hợp vào chỗ chấm.
$\frac{2}{3} = \frac{{......}}{6}$ ; $\frac{6}{{15}} = \frac{{.......}}{5}$
$\frac{{12}}{{18}} = \frac{2}{{......}}$ ; $\frac{7}{9} = \frac{{......}}{{54}}$
Phương pháp giải:
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
Lời giải chi tiết:
$\frac{2}{3} = \frac{4}{6}$ ; $\frac{6}{{15}} = \frac{2}{5}$
$\frac{{12}}{{18}} = \frac{2}{3}$ ; $\frac{7}{9} = \frac{{42}}{{54}}$
a) Viết số thích hợp vào chỗ chấm.
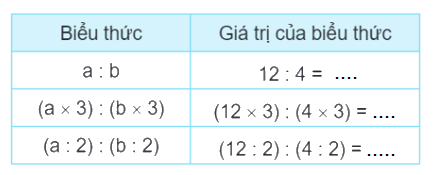
b) >, <, =?
a : b ........ (a x 3) : (b x 3)
a : b ........ (a : 2) : (b : 2)
Phương pháp giải:
a) Tính giá trị biểu thức.
b) Dựa vào nhận xét ở câu a để điền dấu thích hợp.
Lời giải chi tiết:
a)

b)
a : b = (a x 3) : (b x 3)
a : b = (a : 2) : (b : 2)
Viết số thích hợp vào chỗ chấm.
a) $\frac{8}{{12}} = \frac{{.....}}{3} = \frac{4}{{......}}$
b) $\frac{2}{3} = \frac{6}{{......}} = \frac{{......}}{{18}} = \frac{{.....}}{{45}}$
Cộng các số đã viết ở câu b được kết quả là: .............
Phương pháp giải:
Áp dụng tính chất cơ bản của phân số để tìm các số bị che lấp.
Lời giải chi tiết:

Bài 55 thuộc chương trình Toán 4, tập trung vào việc củng cố và mở rộng kiến thức về tính chất cơ bản của phân số. Hiểu rõ tính chất này là nền tảng quan trọng để thực hiện các phép toán với phân số một cách chính xác và hiệu quả.
Tính chất cơ bản của phân số được phát biểu như sau: Nếu ta nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0, thì ta được một phân số bằng phân số ban đầu.
Ví dụ: \frac{2}{3} = \frac{2 \times 2}{3 \times 2} = \frac{4}{6}
Ngược lại, nếu ta chia cả tử số và mẫu số của một phân số cho cùng một số tự nhiên (khác 0), thì ta cũng được một phân số bằng phân số ban đầu. Đây chính là cách rút gọn phân số.
Ví dụ: \frac{4}{6} = \frac{4 \div 2}{6 \div 2} = \frac{2}{3}
Dưới đây là lời giải chi tiết cho các bài tập trong Vở thực hành Toán 4 trang 52:
Hướng dẫn: Sử dụng tính chất cơ bản của phân số để tìm số thích hợp điền vào chỗ trống. Chú ý chọn các số tự nhiên khác 0.
Hướng dẫn: Tìm ước chung lớn nhất (ƯCLN) của tử số và mẫu số, sau đó chia cả tử số và mẫu số cho ƯCLN đó.
Hướng dẫn: Quy đồng mẫu số của các phân số để so sánh. Hoặc sử dụng tính chất cơ bản của phân số để biến đổi các phân số về dạng có cùng tử số hoặc mẫu số.
Để hiểu sâu hơn về tính chất cơ bản của phân số, các em có thể thực hiện thêm các bài tập sau:
Bài 55 đã giúp các em củng cố kiến thức về tính chất cơ bản của phân số. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán liên quan đến phân số một cách dễ dàng và chính xác hơn. Hãy luyện tập thường xuyên để đạt kết quả tốt nhất!