Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 71 Sách bài tập Toán 6 – Chân trời sáng tạo. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và tự tin làm bài tập về nhà.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp đáp án chính xác và dễ hiểu nhất.
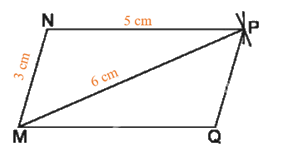
Nêu cách vẽ hình bình hành MNPQ với MN = 3 cm, NP = 5 cm, MP = 6 cm.
Đề bài
Nêu cách vẽ hình bình hành MNPQ với MN = 3 cm, NP = 5 cm, MP = 6 cm.
Lời giải chi tiết
- Dùng thước thẳng vẽ đoạn thẳng MN = 3 cm.
- Dùng compa vẽ một phần đường tròn tâm M bán kính 6 cm. Vẽ một phần đường tròn tâm N bán kính 5 cm. Hai phần đường tròn trên cắt nhau tại điểm P (xem hình dưới).
- Nối N với P. Từ M kẻ đường thẳng MQ song song với NP và MQ = 5 cm.
- Nối P với Q ta được tứ giác MNPQ là hình bình hành cần vẽ.
Bài 9 trang 71 Sách bài tập Toán 6 – Chân trời sáng tạo thuộc chương trình học Toán 6, tập trung vào việc ôn tập và củng cố kiến thức về các phép tính với số tự nhiên, đặc biệt là các bài toán liên quan đến ước và bội. Mục tiêu chính của bài tập này là giúp học sinh rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Bài 9 bao gồm các dạng bài tập sau:
Để tìm các ước chung của 12 và 18, ta thực hiện các bước sau:
Để tìm các bội chung của 4 và 6, ta thực hiện các bước sau:
Để giải bài toán này, ta cần tìm ước chung lớn nhất (ƯCLN) của 24 và 30.
ƯCLN(24, 30) = 6
Vậy, cô giáo có thể chia được nhiều nhất 6 nhóm. Mỗi nhóm có 24/6 = 4 học sinh nam và 30/6 = 5 học sinh nữ.
Để củng cố kiến thức về ước và bội, các em có thể tự giải thêm các bài tập sau:
Bài 9 trang 71 Sách bài tập Toán 6 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về ước và bội. Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên đây, các em sẽ tự tin hơn khi làm bài tập về nhà và đạt kết quả tốt trong môn Toán.