Chào mừng các em học sinh đến với lời giải chi tiết bài 3 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, mang đến những tài liệu học tập chất lượng và hữu ích.
Tính chu vi của hình bên, biết BCDE là hình chữ nhật có diễn tích 135({m^2}), BC = 15 m, ABGK là hình chữ nhật có diện tích 180 mét vuông, BE = EG.
Đề bài
Tính chu vi của hình bên, biết BCDE là hình chữ nhật có diễn tích 135\({m^2}\), BC = 15 m, ABGK là hình chữ nhật có diện tích 180 \({m^2}\), BE = EG.
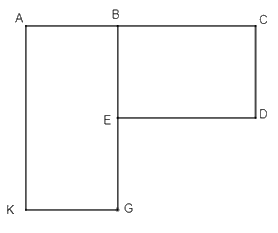
Phương pháp giải - Xem chi tiết
Bước 1: Tính BE dựa vào diện tích BCDE và cạnh BC đã biết
Bước 2: Tính các cạnh còn lại
Bước 3: Tính chu vi
Lời giải chi tiết
Ta có: diện tích hình chữ nhật BCDE là BC. BE = 135 (\({m^2}\)), mà BC = 15 m.
\( \Rightarrow \)BE = 135 : 15 = 9 (m)
Lại có:
EG = BE; AK = BG = 2BE
\( \Rightarrow \) EG = 9m; AK = 18m
Mà diện tích hình chữ nhật ABGK là AB. AK = 180 (\({m^2}\))
\( \Rightarrow \) AB = 180 : 18 = 10 (m)
Vậy chu vi của hình đã cho là:
P = AK + AB + BC + CD + DE + EG + KG = 18 + 10 + 15 + 9 + 15 + 9 + 10 = 86 (m)
Bài 3 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo thuộc chương học về các phép tính với số tự nhiên, cụ thể là các bài tập liên quan đến phép chia hết, chia có dư và tính chất chia hết. Mục tiêu của bài tập này là giúp học sinh củng cố kiến thức về các khái niệm này và rèn luyện kỹ năng giải toán cơ bản.
Bài 3 bao gồm một số câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Để giải câu a), học sinh cần hiểu rõ khái niệm chia hết. Một số a chia hết cho một số b nếu phép chia a cho b cho kết quả là một số tự nhiên. Ví dụ, 12 chia hết cho 3 vì 12 : 3 = 4.
Áp dụng kiến thức này, học sinh cần kiểm tra xem số đã cho có chia hết cho số chia hay không. Nếu chia hết, kết quả là một số tự nhiên. Nếu không chia hết, kết quả sẽ là một số thập phân.
Câu b) yêu cầu học sinh tìm số chia và số dư trong phép chia. Để làm được điều này, học sinh cần nhớ lại công thức liên hệ giữa số bị chia, số chia, thương và số dư: Số bị chia = Số chia x Thương + Số dư. Trong đó, số dư phải nhỏ hơn số chia.
Học sinh cần phân tích đề bài để xác định số bị chia, thương và số chia (nếu có). Sau đó, sử dụng công thức trên để tính toán số dư.
Câu c) thường là một bài toán ứng dụng thực tế, yêu cầu học sinh vận dụng kiến thức về phép chia để giải quyết. Học sinh cần đọc kỹ đề bài, xác định các yếu tố liên quan đến phép chia và lập phương trình hoặc biểu thức phù hợp để giải quyết bài toán.
Ví dụ: Cho số 25 và số 7. Hãy tìm số chia và số dư khi chia 25 cho 7.
Giải:
Ta có: 25 = 7 x 3 + 4
Vậy, số chia là 7, thương là 3 và số dư là 4.
Để hiểu rõ hơn về các phép tính với số tự nhiên, học sinh có thể tham khảo thêm:
Bài 3 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép chia hết và chia có dư. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập một cách hiệu quả. Chúc các em học tốt!