Chào mừng các em học sinh đến với lời giải chi tiết bài 5 trang 95 sách bài tập Toán 6 – Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em hiểu bài và làm bài tập một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải bài tập này ngay nhé!
Hãy đọc dữ liệu thống kê từ biểu đồ tranh sau đây và ghi vào bảng thống kê tương ứng. Số học sinh nữ của các lớp khối 6 trường THCS Hai Bà Trưng
Đề bài
Hãy đọc dữ liệu thống kê từ biểu đồ tranh sau đây và ghi vào bảng thống kê tương ứng.
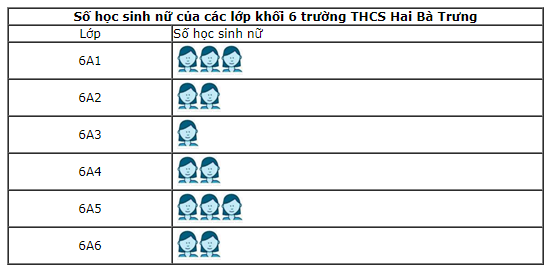
(  = 5 học sinh nữ)
= 5 học sinh nữ)
Phương pháp giải - Xem chi tiết
Quy đổi các biểu tượng sang số, từ đó suy ra số học sinh nữ mỗi lớp tương ứng.
Lời giải chi tiết
Số học sinh nữ các lớp khối 6 trường THCS Hai Bà Trưng | |
Lớp | Số học sinh nữ |
6A1 | 15 |
6A2 | 10 |
6A3 | 5 |
6A4 | 10 |
6A5 | 15 |
6A6 | 10 |
Bài 5 trang 95 sách bài tập Toán 6 – Chân trời sáng tạo thuộc chương trình học Toán 6, tập trung vào việc ôn tập và củng cố kiến thức về các phép tính với số tự nhiên, các khái niệm về bội và ước, cũng như các bài toán liên quan đến ứng dụng thực tế. Mục tiêu của bài tập này là giúp học sinh rèn luyện kỹ năng giải toán, tư duy logic và khả năng vận dụng kiến thức vào giải quyết các vấn đề.
Bài 5 bao gồm các dạng bài tập sau:
Để giải bài 5 trang 95 sách bài tập Toán 6 – Chân trời sáng tạo một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Đề bài: Tính giá trị của biểu thức: 23 + 32 - 5
Giải:
23 + 32 - 5 = 8 + 9 - 5 = 17 - 5 = 12
Vậy, giá trị của biểu thức là 12.
Đề bài: Tìm BCNN của 12 và 18.
Giải:
Phân tích các số ra thừa số nguyên tố:
BCNN(12, 18) = 22 . 32 = 4 . 9 = 36
Vậy, BCNN của 12 và 18 là 36.
Đề bài: Tìm UCLN của 24 và 36.
Giải:
Phân tích các số ra thừa số nguyên tố:
UCLN(24, 36) = 22 . 3 = 4 . 3 = 12
Vậy, UCLN của 24 và 36 là 12.
Để học Toán 6 – Chân trời sáng tạo hiệu quả, các em nên:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài 5 trang 95 sách bài tập Toán 6 – Chân trời sáng tạo, các em học sinh đã hiểu rõ hơn về bài tập này và có thể tự tin giải các bài tập tương tự. Chúc các em học tập tốt!