Chào mừng các em học sinh đến với lời giải chi tiết bài 2 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình học tập và ôn luyện môn Toán.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin giải quyết các bài tập tương tự.
Tính chu vi và diện tích của hình bên, biết AB = 7 cm, BC = 2 cm, CD = 3 cm và DE = 3 cm.
Đề bài
Tính chu vi và diện tích của hình bên, biết AB = 7 cm, BC = 2 cm, CD = 3 cm và DE = 3 cm.
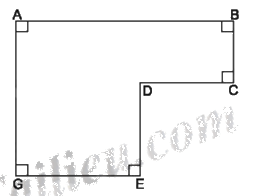
Phương pháp giải - Xem chi tiết
Tính đoạn AG, GE để suy ra chu vi.
Chia hình đã cho thành 2 hình chữ nhật để tính diện tích.
Lời giải chi tiết
Ta chia hình đã cho thành hai hình chữ nhật như hình dưới đây:
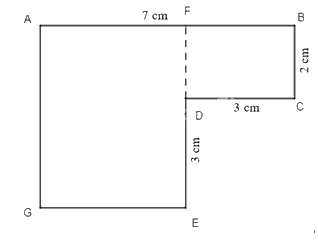
Dễ thấy: AG = BC + DE = 2 + 3 = 5 (cm)
GE = AF = AB – FB = AB – DC = 7 – 3 = 4 (cm)
Vậy chu vi hình trên là:
P = AB + BC + CD + DE + EG + GA = 7 + 2 + 3 + 4 + 5 = 21 (cm)
Diện tích hình chữ nhật AFEG là: AG . GE = 5 . 4 = 20 (\(c{m^2}\))
Diện tích hình chữ nhật FBND là: BC . CD = 2 . 3 = 6 (\(c{m^2}\))
Vậy diện tích của hình đã cho là: 20 + 6 = 26 (\(c{m^2}\))
Bài 2 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo thuộc chương trình học Toán 6, tập trung vào việc rèn luyện kỹ năng thực hành các phép tính với số tự nhiên, đặc biệt là các bài toán liên quan đến phép chia có dư. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Bài 2 bao gồm một số câu hỏi và bài tập yêu cầu học sinh:
Để giải câu a, ta thực hiện phép chia 125 cho 7. Kết quả là:
125 : 7 = 17 dư 6
Vậy, thương là 17 và số dư là 6.
Tương tự như câu a, ta thực hiện phép chia 234 cho 11. Kết quả là:
234 : 11 = 21 dư 3
Vậy, thương là 21 và số dư là 3.
Để kiểm tra xem 345 có chia hết cho 15 hay không, ta thực hiện phép chia 345 cho 15. Nếu kết quả là một số nguyên thì 345 chia hết cho 15, ngược lại thì không.
345 : 15 = 23
Vì kết quả là một số nguyên (23) nên 345 chia hết cho 15.
Phép chia có dư là một khái niệm quan trọng trong Toán học, được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống. Ví dụ, khi chia một số lượng lớn kẹo cho một nhóm bạn, ta cần biết số kẹo mỗi bạn được nhận và số kẹo còn dư.
Để củng cố kiến thức về phép chia có dư, các em có thể tự giải các bài tập sau:
Khi giải các bài tập về phép chia có dư, các em nên:
Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em học sinh đã nắm vững kiến thức và kỹ năng giải bài 2 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!