Chào mừng các em học sinh đến với lời giải chi tiết bài 9 trang 67 Sách bài tập Toán 6 – Chân trời sáng tạo. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 6.
Chúng tôi sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, logic, giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Cho lục giác đều ABCDEG a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần. b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
Phương pháp giải:
b) Tính tổng đường chéo. Dựa vào số đường chéo được đếm 2 lần để suy ra số đường chéo của lục giác.
Lời giải chi tiết:
b) Tổng số đường chéo kể cả các đường được đếm 2 lần là:
3 . 6 = 18 (đường)
Mà mỗi đường chéo đều đước đếm 2 lần, do đó số đường chéo của lục giác là:
18 : 2 = 9 (đường chéo)
a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần.
Phương pháp giải:
a) Bước 1: Vẽ lục giác và các đường chéo từ đỉnh A.
Bước 2: Từ hình vẽ suy ra các đường chéo từ các đỉnh còn lại và đếm số đỉnh được đếm 2 lần.
Lời giải chi tiết:
a) Từ đỉnh A có 3 đường chéo là: AC, AD, AE.
Từ đỉnh B có 3 đường chéo là: BD, BE, BG.
Từ đỉnh C có 3 đường chéo là: CE, CG, CA.
Từ đỉnh D có 3 đường chéo là: DG, DA, DB.
Từ đỉnh E có 3 đường chéo là: EA, EB, EC.
Từ đỉnh G có 3 đường chéo là: GB, GC, GD.
Trong đó 9 đường chéo được đếm 2 lần.
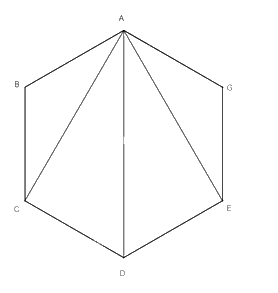
Cho lục giác đều ABCDEG
a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần.
b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần.
Phương pháp giải:
a) Bước 1: Vẽ lục giác và các đường chéo từ đỉnh A.
Bước 2: Từ hình vẽ suy ra các đường chéo từ các đỉnh còn lại và đếm số đỉnh được đếm 2 lần.
Lời giải chi tiết:
a) Từ đỉnh A có 3 đường chéo là: AC, AD, AE.
Từ đỉnh B có 3 đường chéo là: BD, BE, BG.
Từ đỉnh C có 3 đường chéo là: CE, CG, CA.
Từ đỉnh D có 3 đường chéo là: DG, DA, DB.
Từ đỉnh E có 3 đường chéo là: EA, EB, EC.
Từ đỉnh G có 3 đường chéo là: GB, GC, GD.
Trong đó 9 đường chéo được đếm 2 lần.
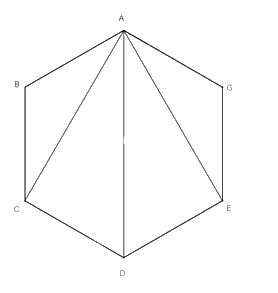
b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.
Phương pháp giải:
b) Tính tổng đường chéo. Dựa vào số đường chéo được đếm 2 lần để suy ra số đường chéo của lục giác.
Lời giải chi tiết:
b) Tổng số đường chéo kể cả các đường được đếm 2 lần là:
3 . 6 = 18 (đường)
Mà mỗi đường chéo đều đước đếm 2 lần, do đó số đường chéo của lục giác là:
18 : 2 = 9 (đường chéo)
Bài 9 trang 67 Sách bài tập Toán 6 – Chân trời sáng tạo thuộc chương trình học Toán 6, tập trung vào việc rèn luyện kỹ năng thực hiện các phép tính với số tự nhiên, đặc biệt là các phép tính liên quan đến lũy thừa và thứ tự thực hiện các phép tính. Bài tập này giúp học sinh củng cố kiến thức đã học và phát triển tư duy logic, khả năng giải quyết vấn đề.
Bài 9 bao gồm các dạng bài tập sau:
a) 32 + 23
Giải:
32 = 3 x 3 = 9
23 = 2 x 2 x 2 = 8
Vậy, 32 + 23 = 9 + 8 = 17
b) 52 - 42
Giải:
52 = 5 x 5 = 25
42 = 4 x 4 = 16
Vậy, 52 - 42 = 25 - 16 = 9
a) 23 và 32
Giải:
23 = 2 x 2 x 2 = 8
32 = 3 x 3 = 9
Vì 8 < 9 nên 23 < 32
b) 52 và 25
Giải:
52 = 5 x 5 = 25
25 = 2 x 2 x 2 x 2 x 2 = 32
Vì 25 < 32 nên 52 < 25
Việc nắm vững kiến thức và kỹ năng giải bài tập trong bài 9 trang 67 Sách bài tập Toán 6 – Chân trời sáng tạo là rất quan trọng đối với học sinh lớp 6. Nó giúp các em:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong bài viết này, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 6. Chúc các em học tập tốt và đạt kết quả cao!