Bài học này sẽ cung cấp kiến thức nền tảng và nâng cao về các góc tạo bởi một đường thẳng cắt hai đường thẳng trong hình học. Chúng ta sẽ cùng nhau khám phá các loại góc đặc biệt như góc so le trong, góc so le ngoài, góc đồng vị và cách xác định chúng.
Nội dung bài học được trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.
Góc so le trong, góc đồng vị, góc trong cùng phía, góc so le ngoài
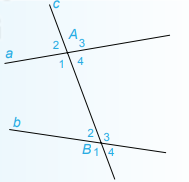
+ Các cặp góc A1 và B3 ; A4 và B2 được gọi là các cặp góc so le trong
+ Các cặp góc A1 và B1 ; A2 và B2 ; A3 và B3 ; A4 và B4 được gọi là các cặp góc đồng vị
+ Các cặp góc A1 và B2 ; A4 và B3 được gọi là các cặp góc trong cùng phía
+ Các cặp góc A2 và B4 ; A3 và B1 được gọi là các cặp góc so le ngoài.
Trong hình học, một vấn đề cơ bản và quan trọng là xét các góc tạo thành khi một đường thẳng cắt hai đường thẳng khác. Việc hiểu rõ các loại góc này và mối quan hệ giữa chúng là nền tảng để giải quyết nhiều bài toán hình học phức tạp hơn.
Khi một đường thẳng (gọi là đường cắt) cắt hai đường thẳng khác, nó tạo ra 8 góc xung quanh điểm giao nhau. Các góc này được phân loại dựa trên vị trí tương đối của chúng:
Các góc tạo bởi một đường thẳng cắt hai đường thẳng có những mối quan hệ quan trọng sau:
Các mối quan hệ giữa các góc tạo bởi một đường thẳng cắt hai đường thẳng được sử dụng để xác định hai đường thẳng có song song hay không:
Ví dụ 1: Cho hình vẽ, biết góc A1 = 60 độ. Tính các góc còn lại.
Giải:
Bài 1: Cho hình vẽ, biết góc B1 = 70 độ. Tính góc A1.
Bài 2: Hai đường thẳng a và b bị cắt bởi đường thẳng c. Biết góc so le trong bằng 50 độ. Hỏi hai đường thẳng a và b có song song không? Vì sao?
Kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng có ứng dụng rộng rãi trong thực tế, chẳng hạn như:
Việc nắm vững kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng là rất quan trọng trong học tập và ứng dụng thực tế. Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc giải quyết các bài toán hình học.