Hình hộp chữ nhật là một hình khối trong không gian, được tạo thành bởi sáu mặt hình chữ nhật. Đây là một trong những hình học cơ bản và quan trọng trong chương trình toán học, đặc biệt là ở cấp tiểu học và trung học cơ sở.
Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ về hình hộp chữ nhật, bao gồm cách tính diện tích xung quanh, diện tích toàn phần và thể tích. Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa để bạn có thể nắm vững kiến thức một cách nhanh chóng.
Hình hộp chữ nhật, diện tích xung quanh, diện tích toàn phần, thể tích hình hộp chữ nhật
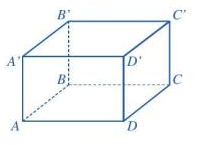
a) Hình hộp chữ nhật có:
- 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình chữ nhật.
- Các cạnh bên bằng nhau.
b) Diện tích xung quanh, diện tích toàn phần, thể tích của hình hộp chữ nhật:
Hình hộp chữ nhật có chiều dài a, chiều rộng b, chiều cao có:
\(S_{xq}=2(a+b)h\);
\(S_{tp}=S_{xq} + S_{2 đáy}=2(a+b)h+2ab\);
\(V = a.b.c\)
Hình hộp chữ nhật là hình khối có sáu mặt đều là hình chữ nhật. Các mặt đối diện song song và bằng nhau. Để hiểu rõ hơn về hình hộp chữ nhật, chúng ta cần nắm vững các yếu tố cơ bản:
Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích của bốn mặt bên. Công thức tính diện tích xung quanh (Sxq) như sau:
Sxq = 2 * (a + b) * c
Trong đó:
Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích của tất cả sáu mặt. Công thức tính diện tích toàn phần (Stp) như sau:
Stp = 2 * (a * b + a * c + b * c)
Hoặc có thể tính bằng công thức:
Stp = Sxq + 2 * (a * b)
Trong đó:
Thể tích của hình hộp chữ nhật là lượng không gian mà hình hộp chữ nhật chiếm giữ. Công thức tính thể tích (V) như sau:
V = a * b * c
Trong đó:
Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 3cm và chiều cao 4cm. Hãy tính:
Giải:
1. Diện tích xung quanh: Sxq = 2 * (5 + 3) * 4 = 64 cm2
2. Diện tích toàn phần: Stp = 2 * (5 * 3 + 5 * 4 + 3 * 4) = 94 cm2
3. Thể tích: V = 5 * 3 * 4 = 60 cm3
1. Một bể cá hình hộp chữ nhật có chiều dài 80cm, chiều rộng 40cm và chiều cao 50cm. Tính thể tích nước tối đa có thể chứa trong bể.
2. Một phòng học hình hộp chữ nhật có chiều dài 9m, chiều rộng 6m và chiều cao 4m. Người ta muốn quét vôi tất cả các mặt tường của phòng học. Tính diện tích cần quét vôi.
3. Một hộp quà hình hộp chữ nhật có diện tích toàn phần là 376cm2, chiều dài 10cm, chiều rộng 8cm. Tính chiều cao của hộp quà.
Hình hộp chữ nhật xuất hiện rất nhiều trong cuộc sống hàng ngày, ví dụ như:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về hình hộp chữ nhật. Việc nắm vững các công thức tính diện tích xung quanh, diện tích toàn phần và thể tích sẽ giúp bạn giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.