Trong chương trình học Toán lớp 7, việc nắm vững các trường hợp bằng nhau của tam giác là vô cùng quan trọng. Một trong những trường hợp đó là 'Trường hợp bằng nhau cạnh góc vuông – góc nhọn kề'.
Bài viết này sẽ cung cấp kiến thức đầy đủ, dễ hiểu về trường hợp bằng nhau này, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức và áp dụng vào giải bài tập một cách hiệu quả.
Trường hợp bằng nhau cạnh góc vuông – góc nhọn kề
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g.c.g)
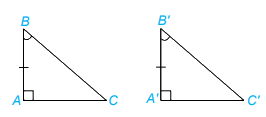
Xét tam giác ABC và A’B’C’, ta có:
\(\widehat A = \widehat {A'}( = 90^\circ )\)
AB = A’B’
\(\widehat B = \widehat {B'}\)
Vậy \(\Delta ABC = \Delta A'B'C'\) ( g.c.g)
Trong hình học, hai tam giác được gọi là bằng nhau nếu chúng có tất cả các cạnh và các góc tương ứng bằng nhau. Có nhiều trường hợp để chứng minh hai tam giác bằng nhau, và một trong số đó là trường hợp bằng nhau cạnh góc vuông – góc nhọn kề.
Định nghĩa: Nếu hai tam giác ABC và A'B'C' có:
Thì hai tam giác ABC và A'B'C' bằng nhau.
Giải thích: Trường hợp này dựa trên việc xác định duy nhất một tam giác khi biết hai cạnh và góc xen giữa chúng. Nếu hai tam giác có hai cạnh bằng nhau và góc xen giữa hai cạnh đó bằng nhau, thì hai tam giác đó hoàn toàn giống nhau.
Ví dụ 1: Cho tam giác ABC và tam giác DEF có AB = DE, ∠A = ∠D, AC = DF. Chứng minh rằng tam giác ABC bằng tam giác DEF.
Giải:
Ví dụ 2: Cho hình vẽ, biết AB = CD, ∠BAC = ∠DCA. Chứng minh rằng tam giác ABC bằng tam giác CDA.
(Hình vẽ minh họa với hai tam giác ABC và CDA có chung cạnh AC, AB = CD, ∠BAC = ∠DCA)
Giải:
Trường hợp bằng nhau cạnh góc vuông – góc nhọn kề được ứng dụng rộng rãi trong việc giải các bài toán chứng minh hai tam giác bằng nhau, từ đó suy ra các yếu tố tương ứng bằng nhau (cạnh, góc).
Ví dụ: Trong các bài toán liên quan đến tam giác cân, tam giác vuông, việc chứng minh hai tam giác bằng nhau thường là bước quan trọng để tìm ra các góc hoặc cạnh bằng nhau.
Bài 1: Cho tam giác PQR và tam giác XYZ có PQ = XY, ∠P = ∠X, PR = XZ. Chứng minh rằng tam giác PQR bằng tam giác XYZ.
Bài 2: Cho hình vẽ, biết AB = CD, ∠ABD = ∠CDB. Chứng minh rằng tam giác ABD bằng tam giác CDB.
(Hình vẽ minh họa với hai tam giác ABD và CDB có chung cạnh BD, AB = CD, ∠ABD = ∠CDB)
Trường hợp bằng nhau cạnh góc vuông – góc nhọn kề là một công cụ quan trọng trong hình học, giúp chúng ta chứng minh hai tam giác bằng nhau và giải quyết các bài toán liên quan. Việc nắm vững định nghĩa, điều kiện và ứng dụng của trường hợp này sẽ giúp bạn học Toán hiệu quả hơn.