Chủ đề 'Hai tam giác bằng nhau' là một trong những kiến thức cơ bản và quan trọng trong chương trình học Toán Hình học. Việc nắm vững các trường hợp bằng nhau của tam giác giúp học sinh giải quyết các bài toán chứng minh hình học một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, bài tập đa dạng và phương pháp giải bài tập 'Hai tam giác bằng nhau' một cách dễ hiểu, giúp bạn tự tin chinh phục môn Toán.
Hai tam giác bằng nhau
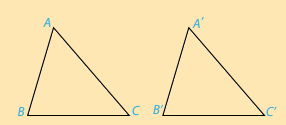
Hai tam giác ABC và A’B’C’ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, tức là:
AB = A’B’ ; AC = A’C’ ; BC = B’C’ và \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
Ta viết: \(\Delta ABC = \Delta A'B'C'\)
Nếu 2 tam giác bằng nhau, ta suy ra tất cả các cạnh, các góc tương ứng bằng nhau.
Trong hình học, hai tam giác được gọi là bằng nhau nếu chúng có cùng kích thước và hình dạng. Điều này có nghĩa là tất cả các cạnh và các góc tương ứng của chúng phải bằng nhau. Việc chứng minh hai tam giác bằng nhau là một kỹ năng quan trọng trong giải toán hình học, và có nhiều phương pháp khác nhau để thực hiện điều này.
Có ba trường hợp cơ bản để chứng minh hai tam giác bằng nhau:
Việc chứng minh hai tam giác bằng nhau có rất nhiều ứng dụng trong giải toán hình học. Một số ứng dụng phổ biến bao gồm:
Ví dụ 1: Cho tam giác ABC và tam giác DEF có AB = DE, BC = EF, và AC = DF. Chứng minh rằng tam giác ABC bằng tam giác DEF.
Giải:
Vì AB = DE, BC = EF, và AC = DF (giả thiết), nên theo trường hợp bằng nhau cạnh - cạnh - cạnh (c-c-c), ta có tam giác ABC bằng tam giác DEF.
Ví dụ 2: Cho tam giác MNP và tam giác RST có MN = RS, góc N = góc S, và NP = ST. Chứng minh rằng tam giác MNP bằng tam giác RST.
Giải:
Vì MN = RS, góc N = góc S, và NP = ST (giả thiết), nên theo trường hợp bằng nhau cạnh - góc - cạnh (c-g-c), ta có tam giác MNP bằng tam giác RST.
Để củng cố kiến thức về hai tam giác bằng nhau, bạn có thể thực hành các bài tập sau:
Chủ đề 'Hai tam giác bằng nhau' là một phần quan trọng của chương trình học Toán Hình học. Việc nắm vững các trường hợp bằng nhau của tam giác và ứng dụng chúng trong giải toán là một kỹ năng cần thiết cho học sinh. Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học Toán.