Trong chương trình học Toán lớp 7, kiến thức về đường thẳng song song và các tính chất liên quan là một phần quan trọng của môn Hình học. Việc nắm vững các tính chất này không chỉ giúp học sinh giải quyết các bài tập một cách chính xác mà còn là nền tảng cho các kiến thức nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, bài giảng chi tiết và bài tập thực hành đa dạng để giúp bạn hiểu rõ về tính chất của hai đường thẳng song song.
Tính chất của hai đường thẳng song song
Nếu một đường thẳng cắt hai đường thẳng song song thì:
+ Hai góc so le trong bằng nhau
+ Hai góc đồng vị bằng nhau
+ Hai góc trong cùng phía bằng nhau
+ Hai góc so le ngoài bằng nhau
Chú ý:
+ Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
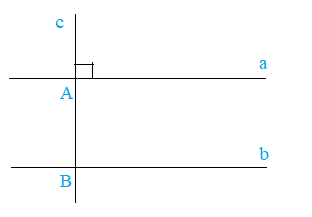
Nếu c \( \bot \) a, a // b thì c \( \bot \) b
+ Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Trong hình học, hai đường thẳng được gọi là song song khi chúng không có điểm chung nào. Để hiểu rõ hơn về mối quan hệ giữa các đường thẳng song song, chúng ta cần nắm vững các tính chất quan trọng. Bài viết này sẽ trình bày chi tiết về các tính chất này, kèm theo ví dụ minh họa và bài tập áp dụng để giúp bạn nắm vững kiến thức.
Hai đường thẳng được gọi là song song nếu chúng không có điểm chung. Ký hiệu: a // b (đọc là a song song với b).
Có ba tính chất cơ bản liên quan đến hai đường thẳng song song và một đường thẳng cắt ngang:
Có ba cách để chứng minh hai đường thẳng song song:
Ví dụ 1: Cho hình vẽ, biết ∠A1 = 60°. Chứng minh a // b.
Giải:
∠A1 và ∠B1 là hai góc so le trong. Vì ∠A1 = 60° và ∠B1 = 60° nên ∠A1 = ∠B1. Do đó, a // b (theo tính chất góc so le trong).
Ví dụ 2: Cho hình vẽ, biết ∠A2 = 120°. Chứng minh a // b.
Giải:
∠A2 và ∠B2 là hai góc đồng vị. Vì ∠A2 = 120° và ∠B2 = 120° nên ∠A2 = ∠B2. Do đó, a // b (theo tính chất góc đồng vị).
Bài 1: Cho hình vẽ, biết ∠A3 = 135°. Tính ∠B3 và chứng minh a // b.
Bài 2: Cho hình vẽ, biết ∠A4 = 45°. Tính ∠B4 và chứng minh a // b.
Bài 3: Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c cắt a tại điểm M và cắt b tại điểm N. Biết ∠AMN = 70°. Tính các góc còn lại tạo bởi đường thẳng c và hai đường thẳng a, b.
Các tính chất của hai đường thẳng song song có ứng dụng rộng rãi trong thực tế và trong các lĩnh vực khác của toán học, như:
Khi áp dụng các tính chất của hai đường thẳng song song, cần chú ý:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về tính chất của hai đường thẳng song song. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng thành thạo vào giải các bài tập.