Trong hình học, sự đồng quy của ba đường phân giác là một tính chất quan trọng của tam giác. Nó khẳng định rằng ba đường phân giác của một tam giác luôn đồng quy tại một điểm duy nhất, được gọi là tâm đường tròn nội tiếp của tam giác.
Bài viết này trên giaitoan.edu.vn sẽ cung cấp cho bạn kiến thức đầy đủ và chi tiết về sự đồng quy này, bao gồm định nghĩa, tính chất, chứng minh và ứng dụng trong giải toán.
3 đường phân giác của tam giác đồng quy
Trong tam giác ABC, tia phân giác của góc A cắt cạnh BC tại D thì đoạn thẳng AD được gọi là đường phân giác của tam giác ABC.
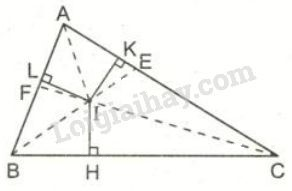
Định lí: Ba đường phân giác của một tam giác đồng quy tại 1 điểm. Điểm này cách đều ba cạnh của tam giác đó.
Giao điểm của ba đường phân giác gọi là tâm đường tròn nội tiếp tam giác.
Trong hình học phẳng, tam giác là một trong những hình cơ bản nhất. Nghiên cứu về tam giác không chỉ quan trọng trong toán học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác như kiến trúc, kỹ thuật, và khoa học tự nhiên. Một trong những tính chất quan trọng của tam giác là sự đồng quy của ba đường phân giác.
Đường phân giác của một góc trong tam giác là đường thẳng đi qua đỉnh của góc đó và chia góc đó thành hai góc bằng nhau. Điểm giao nhau của ba đường phân giác trong một tam giác được gọi là tâm đường tròn nội tiếp (incenter) của tam giác. Tâm đường tròn nội tiếp là tâm của đường tròn nội tiếp tam giác, đường tròn tiếp xúc với cả ba cạnh của tam giác.
Tính chất cơ bản nhất của sự đồng quy ba đường phân giác là: Ba đường phân giác của một tam giác đồng quy tại một điểm. Điểm đồng quy này, như đã đề cập, là tâm đường tròn nội tiếp của tam giác. Tâm đường tròn nội tiếp cách đều ba cạnh của tam giác. Khoảng cách từ tâm đường tròn nội tiếp đến mỗi cạnh là bán kính của đường tròn nội tiếp (r).
Có nhiều cách để chứng minh sự đồng quy của ba đường phân giác. Một trong những cách phổ biến nhất là sử dụng tính chất của đường phân giác và các tam giác đồng dạng.
Sự đồng quy của ba đường phân giác có nhiều ứng dụng trong giải toán hình học, đặc biệt là trong các bài toán liên quan đến tính chất của tam giác, đường tròn nội tiếp và các yếu tố liên quan.
Ví dụ: Cho tam giác ABC có AB = 5cm, BC = 7cm, AC = 8cm. Tính độ dài đường phân giác AD.
Giải:
Áp dụng công thức tính độ dài đường phân giác AD:
AD2 = AB * AC - BD * CD
Theo tính chất đường phân giác, BD/CD = AB/AC = 5/8
Mà BD + CD = BC = 7cm
Suy ra BD = (5/13) * 7 = 35/13 cm và CD = (8/13) * 7 = 56/13 cm
Thay vào công thức, ta có: AD2 = 5 * 8 - (35/13) * (56/13) = 40 - 1960/169 = (6760 - 1960)/169 = 4800/169
Vậy AD = √(4800/169) = (40√3)/13 cm
Sự đồng quy của ba đường phân giác là một trong ba điểm đồng quy nổi tiếng của tam giác (cùng với trọng tâm và trực tâm). Mỗi điểm đồng quy này đều có những tính chất và ứng dụng riêng biệt. Việc hiểu rõ mối liên hệ giữa các điểm đồng quy này giúp chúng ta có cái nhìn toàn diện hơn về tam giác và các tính chất của nó.
Sự đồng quy của ba đường phân giác là một tính chất cơ bản nhưng vô cùng quan trọng trong hình học tam giác. Nắm vững tính chất này và các ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán hình học một cách hiệu quả và chính xác. Hy vọng bài viết này trên giaitoan.edu.vn đã cung cấp cho bạn những kiến thức hữu ích và đầy đủ về chủ đề này.