Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về hình lăng trụ đứng tứ giác, bao gồm định nghĩa, các yếu tố, công thức tính diện tích xung quanh, diện tích toàn phần và thể tích.
Chúng tôi tại giaitoan.edu.vn luôn cố gắng mang đến những bài học toán online chất lượng, dễ hiểu và đầy đủ nhất.
Hình lăng trụ đứng tứ giác, diện tích xung quanh, thể tích hình lăng trụ đứng tứ giác
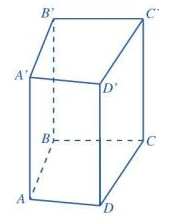
a) Hình lăng trụ đứng tứ giác có:
- Có 8 đỉnh
- 2 mặt đáy cùng là tứ giác và song song với nhau, 4 mặt bên là các hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao là độ dài một cạnh bên.
Chú ý: Hình hộp chữ nhật cũng là một hình lăng trụ đứng tứ giác.
b) Diện tích xung quanh. Thể tích
Diện tích xung quanh = chu vi đáy . chiều cao
Thể tích = diện tích đáy . chiều cao
Hình lăng trụ đứng tứ giác là hình đa diện có hai đáy là hai tứ giác song song và bằng nhau, các cạnh bên vuông góc với hai đáy. Các mặt bên là các hình chữ nhật.
Diện tích xung quanh của hình lăng trụ đứng tứ giác là tổng diện tích của các mặt bên. Vì các mặt bên là các hình chữ nhật, nên diện tích xung quanh được tính bằng công thức:
Sxq = P * h
Trong đó:
Diện tích toàn phần của hình lăng trụ đứng tứ giác là tổng diện tích xung quanh và diện tích của hai đáy. Công thức tính diện tích toàn phần là:
Stp = Sxq + 2B
Trong đó:
Thể tích của hình lăng trụ đứng tứ giác được tính bằng công thức:
V = B * h
Trong đó:
Cho hình lăng trụ đứng tứ giác có đáy là hình chữ nhật với chiều dài 8cm, chiều rộng 6cm và chiều cao 10cm. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lăng trụ.
Các bài tập về hình lăng trụ đứng tứ giác thường xoay quanh việc tính diện tích xung quanh, diện tích toàn phần và thể tích. Ngoài ra, còn có các bài tập liên quan đến việc xác định các yếu tố của hình lăng trụ, như chiều cao, chu vi đáy, diện tích đáy.
Khi giải các bài tập về hình lăng trụ đứng tứ giác, cần chú ý đến đơn vị đo lường và đảm bảo rằng tất cả các đại lượng đều được biểu diễn bằng cùng một đơn vị. Ngoài ra, cần kiểm tra kỹ các điều kiện của bài toán để lựa chọn công thức phù hợp.
Hình lăng trụ đứng tứ giác xuất hiện trong nhiều ứng dụng thực tế, như các hộp đựng hàng hóa, các tòa nhà, các công trình kiến trúc. Việc hiểu rõ về hình lăng trụ đứng tứ giác giúp chúng ta có thể tính toán các thông số cần thiết trong các ứng dụng này.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về hình lăng trụ đứng tứ giác. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.