Bài viết này sẽ cung cấp kiến thức cơ bản và nâng cao về quan hệ giữa đường vuông góc và đường xiên trong hình học. Chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất và ứng dụng của các khái niệm này trong giải toán.
Nội dung được trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể, giúp bạn nắm vững kiến thức và tự tin giải các bài tập liên quan.
Quan hệ giữa đường vuông góc và đường xiên
a) Khái niệm đường vuông góc và đường xiên
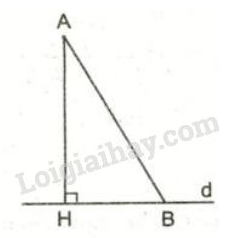
Từ \(A\) không nằm trên \(d\), kẻ một đường thẳng vuông góc với \(d\) tại \(H\). Trên \(d\) lấy điểm \(B\) không trùng với \(H\). Khi đó:
+ Đoạn \(AH\) gọi là đoạn vuông góc hay đường vuông góc kẻ từ \(A\) đến \(d\).
+ Đoạn \(AB\) gọi là đường xiên kẻ từ \(A\) đến \(d\)
b) So sánh đường vuông góc và đường xiên
Định lý: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Trong hình học, đặc biệt là trong chương trình toán lớp 7, việc hiểu rõ quan hệ giữa đường vuông góc và đường xiên là vô cùng quan trọng. Đây là nền tảng để giải quyết nhiều bài toán liên quan đến bất đẳng thức, khoảng cách và các ứng dụng thực tế khác.
Đây là một trong những nội dung quan trọng nhất khi nói đến quan hệ giữa đường vuông góc và đường xiên. Bất đẳng thức đường xiên phát biểu rằng:
Trong một tam giác vuông, cạnh huyền là cạnh dài nhất.
Hoặc, một cách tổng quát hơn:
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh dài hơn.
Có nhiều cách để chứng minh bất đẳng thức đường xiên. Một trong những cách phổ biến nhất là sử dụng định lý Pythagoras.
Xét tam giác ABC vuông tại A. Theo định lý Pythagoras, ta có: BC2 = AB2 + AC2. Vì AB2 > 0 và AC2 > 0, nên BC2 > AB2 và BC2 > AC2. Suy ra BC > AB và BC > AC. Vậy, cạnh huyền BC là cạnh dài nhất.
Ví dụ 1: Cho tam giác ABC có góc B = 60 độ, góc C = 45 độ. Hỏi cạnh nào dài nhất?
Giải: Vì góc B > góc C, nên cạnh AC > cạnh AB. Góc A = 180 - 60 - 45 = 75 độ. Vì góc A > góc B > góc C, nên cạnh BC > cạnh AC > cạnh AB. Vậy, cạnh BC là cạnh dài nhất.
Ví dụ 2: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính độ dài cạnh BC.
Giải: Theo định lý Pythagoras, ta có: BC2 = AB2 + AC2 = 32 + 42 = 9 + 16 = 25. Suy ra BC = √25 = 5cm.
Đường cao của một tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh xuống cạnh đối diện. Đường cao cũng đóng vai trò quan trọng trong việc xác định quan hệ giữa các cạnh và góc trong tam giác.
Trong một tam giác nhọn, đường cao nằm trong tam giác. Trong một tam giác tù, đường cao nằm ngoài tam giác.
Việc nắm vững kiến thức về quan hệ giữa đường vuông góc và đường xiên là điều kiện cần thiết để học tốt môn hình học. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn tự tin hơn trong việc giải các bài toán liên quan.