Sự đồng quy của ba đường trung tuyến của tam giác

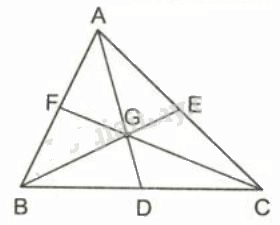
Trong hình học Euclid, đường trung tuyến của một tam giác là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Một tam giác có ba đường trung tuyến, và một tính chất quan trọng là ba đường trung tuyến này đồng quy tại một điểm duy nhất, được gọi là trọng tâm của tam giác.

Định Nghĩa Đường Trung Tuyến và Trọng Tâm

Đường trung tuyến của tam giác ABC, ký hiệu là AM (với M là trung điểm của BC), là đoạn thẳng nối đỉnh A với trung điểm M của cạnh BC. Tương tự, BN và CP là các đường trung tuyến còn lại. Trọng tâm G là giao điểm của ba đường trung tuyến AM, BN và CP.

Chứng Minh Sự Đồng Quy của Ba Đường Trung Tuyến

Có nhiều cách để chứng minh sự đồng quy của ba đường trung tuyến. Một trong những cách phổ biến nhất sử dụng định lý Ceva.

1. Định lý Ceva: Trong tam giác ABC, cho D, E, F lần lượt là các điểm nằm trên các cạnh BC, CA, AB. Ba đoạn thẳng AD, BE, CF đồng quy khi và chỉ khi: (BD/DC) * (CE/EA) * (AF/FB) = 1.
2. Áp dụng vào đường trung tuyến: Vì M, N, P là trung điểm của BC, CA, AB, ta có BD = DC, CE = EA, AF = FB. Do đó, (BD/DC) = 1, (CE/EA) = 1, (AF/FB) = 1.
3. Kết luận: Áp dụng định lý Ceva, ta thấy (1 * 1 * 1) = 1, suy ra ba đường trung tuyến AM, BN, CP đồng quy tại một điểm, chính là trọng tâm G.

Tính Chất của Trọng Tâm

Trọng tâm G có những tính chất quan trọng sau:

• AG = 2/3 AM, BG = 2/3 BN, CG = 2/3 CP.
• GM = 1/3 AM, GN = 1/3 BN, GP = 1/3 CP.
• Trọng tâm G là điểm cân bằng của tam giác.

Ứng Dụng của Sự Đồng Quy Ba Đường Trung Tuyến

Sự đồng quy của ba đường trung tuyến có nhiều ứng dụng trong việc giải toán hình học:

• Chứng minh tính chất hình học: Sử dụng trọng tâm để chứng minh các tính chất liên quan đến tam giác.
• Giải bài toán tìm điểm: Xác định vị trí của trọng tâm trong các bài toán cụ thể.
• Tính toán độ dài đoạn thẳng: Sử dụng các tính chất của trọng tâm để tính toán độ dài các đoạn thẳng liên quan đến đường trung tuyến.

Ví Dụ Minh Họa

Cho tam giác ABC có AB = 6cm, BC = 8cm, CA = 10cm. Hãy tìm độ dài của các đoạn thẳng AM, BG, CG, GM, GN, GP.

Giải:

Vì tam giác ABC vuông tại B (do 6² + 8² = 10²), đường trung tuyến AM có độ dài bằng một nửa cạnh huyền BC, tức là AM = BC/2 = 8/2 = 4cm.

Trọng tâm G chia đường trung tuyến AM theo tỷ lệ 2:1, nên AG = 2/3 AM = 2/3 * 4 = 8/3 cm và GM = 1/3 AM = 1/3 * 4 = 4/3 cm.

Tương tự, ta có thể tính được BG và CG bằng cách sử dụng các công thức tương tự.

Bài Tập Luyện Tập

1. Cho tam giác ABC, M là trung điểm của BC. Chứng minh rằng AM là đường trung tuyến.

2. Cho tam giác ABC, G là trọng tâm. Chứng minh rằng AG = 2GM.

3. Trong tam giác ABC, cho AB = 5cm, BC = 7cm, CA = 8cm. Tính độ dài của các đường trung tuyến AM, BN, CP.

Kết Luận

Sự đồng quy của ba đường trung tuyến là một tính chất cơ bản và quan trọng trong hình học tam giác. Việc nắm vững lý thuyết, chứng minh và ứng dụng của tính chất này sẽ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của bạn tại giaitoan.edu.vn.