Bài học này sẽ cung cấp cho bạn kiến thức nền tảng về tia phân giác của một góc, một khái niệm quan trọng trong hình học.
Chúng ta sẽ cùng tìm hiểu định nghĩa, các tính chất cơ bản và cách ứng dụng tia phân giác trong giải toán.
Giaitoan.edu.vn mang đến phương pháp học toán online hiệu quả, giúp bạn dễ dàng tiếp thu và vận dụng kiến thức.
Tia nằm giữa 2 cạnh của một góc và tạo với 2 cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
Định nghĩa: Tia nằm giữa 2 cạnh của một góc và tạo với 2 cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
* Tính chất: Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {zOy} = \dfrac{1}{2}.\widehat {xOy}\)
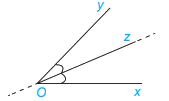
Chú ý: Đường thẳng chứa tia phân giác của một góc là đường phân giác của góc đó.
Tia phân giác của một góc là một khái niệm cơ bản nhưng vô cùng quan trọng trong hình học. Hiểu rõ về tia phân giác sẽ giúp bạn giải quyết nhiều bài toán liên quan đến góc và đường thẳng một cách dễ dàng. Bài viết này sẽ cung cấp một cái nhìn toàn diện về tia phân giác, bao gồm định nghĩa, tính chất, cách vẽ và ứng dụng trong các bài toán thực tế.
Một tia nằm giữa hai cạnh của một góc và tạo với hai cạnh đó hai góc bằng nhau được gọi là tia phân giác của góc đó.
Ví dụ: Xét góc ∠AOB. Nếu tia OC nằm giữa hai cạnh OA và OB sao cho ∠AOC = ∠COB, thì tia OC là tia phân giác của góc ∠AOB.
Tia phân giác của một góc có tính chất quan trọng là chia góc đó thành hai góc bằng nhau. Tính chất này được sử dụng rộng rãi trong việc chứng minh các bài toán hình học.
Định lý: Nếu tia Oy là tia phân giác của góc xOy, thì ∠xOy = ∠yOy.
Có nhiều cách để vẽ tia phân giác của một góc:
Tia phân giác được ứng dụng trong nhiều bài toán hình học, đặc biệt là các bài toán liên quan đến tam giác cân, tam giác đều và các tính chất của góc.
Ví dụ 1: Cho tam giác ABC cân tại A. Tia phân giác của góc BAC cắt BC tại D. Chứng minh rằng AD là đường cao của tam giác ABC.
Giải:
Vì tam giác ABC cân tại A nên AB = AC. Do đó, ∠ABC = ∠ACB.
Vì AD là tia phân giác của góc BAC nên ∠BAD = ∠CAD.
Xét hai tam giác ABD và ACD, ta có:
Do đó, tam giác ABD = tam giác ACD (c.g.c).
Suy ra ∠ADB = ∠ADC.
Mà ∠ADB + ∠ADC = 180° (kề bù) nên ∠ADB = ∠ADC = 90°.
Vậy AD là đường cao của tam giác ABC.
Dưới đây là một số bài tập để bạn luyện tập về tia phân giác:
Khái niệm tia phân giác không chỉ giới hạn trong hình học phẳng. Trong hình học không gian, tia phân giác của một góc nhị diện cũng đóng vai trò quan trọng trong việc xác định mặt phẳng phân giác của góc nhị diện đó.
Tia phân giác của một góc là một khái niệm cơ bản nhưng có nhiều ứng dụng quan trọng trong hình học. Việc nắm vững định nghĩa, tính chất và cách vẽ tia phân giác sẽ giúp bạn giải quyết nhiều bài toán hình học một cách hiệu quả. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về tia phân giác. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.
| Khái niệm | Mô tả |
|---|---|
| Tia phân giác | Tia nằm giữa hai cạnh của một góc và tạo với hai cạnh đó hai góc bằng nhau. |
| Tính chất | Chia góc đó thành hai góc bằng nhau. |