Trong chương trình toán học, đặc biệt là ở lớp 7 và lớp 8, tỉ lệ thức đóng vai trò quan trọng. Hiểu rõ tính chất tỉ lệ thức sẽ giúp học sinh giải quyết các bài toán một cách nhanh chóng và chính xác.
Giaitoan.edu.vn cung cấp bài giảng chi tiết, dễ hiểu về tính chất tỉ lệ thức, cùng với các bài tập thực hành đa dạng để bạn có thể nắm vững kiến thức này.
Tính chất tỉ lệ thức
+ Tính chất 1 (tính chất cơ bản của tỉ lệ thức)
Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)
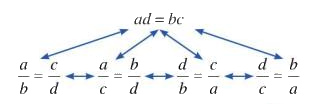
+ Tính chất 2 (điều kiện để bốn số lập thành tỉ lệ thức): Nếu \(ad = bc\) và \(a,b,c,d \ne 0\) thì ta có các tỉ lệ thức
\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)
Ví dụ: Ta có \(\dfrac{3}{6} = \dfrac{9}{{18}} \Rightarrow 3.18 = 9.6\left( { = 54} \right)\)
Vì \(4.9 = 3.12( = 36)\) nên ta có các tỉ lệ thức sau: \(\dfrac{4}{3} = \dfrac{{12}}{9};{\mkern 1mu} \dfrac{3}{4} = \dfrac{9}{{12}};\dfrac{4}{{12}} = \dfrac{3}{9};\dfrac{{12}}{4} = \dfrac{9}{3}\)
Tỉ lệ thức là một khái niệm cơ bản trong toán học, xuất hiện từ những lớp học đầu tiên về phân số và đại số. Hiểu rõ về tỉ lệ thức và các tính chất tỉ lệ thức là nền tảng quan trọng để giải quyết nhiều bài toán phức tạp hơn trong các chương trình học tiếp theo.
Tỉ lệ thức là sự bằng nhau của hai phân số. Nếu ta có hai phân số a/b và c/d, chúng tạo thành một tỉ lệ thức khi và chỉ khi a/b = c/d. Trong đó, a và d là hai số ngoài cùng (gọi là ngoại tỉ), còn b và c là hai số trong cùng (gọi là trung tỉ).
Có ba tính chất tỉ lệ thức cơ bản mà học sinh cần nắm vững:
Các tính chất tỉ lệ thức có rất nhiều ứng dụng trong thực tế và trong các bài toán toán học:
Ví dụ 1: Tìm x trong tỉ lệ thức 2/3 = x/6.
Áp dụng tính chất bắc cầu, ta có thể viết x = (2 * 6) / 3 = 4.
Ví dụ 2: Cho a/b = 3/4 và b/c = 5/6. Tính a/c.
Áp dụng tính chất đảo ngược, ta có a/3 = b/4 và b/5 = c/6. Từ đó, a/c = (a/b) * (b/c) = (3/4) * (5/6) = 15/24 = 5/8.
Để nắm vững các tính chất tỉ lệ thức, bạn cần luyện tập thường xuyên với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Tính chất tỉ lệ thức là một công cụ toán học mạnh mẽ, có ứng dụng rộng rãi trong nhiều lĩnh vực. Việc hiểu rõ và nắm vững các tính chất này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ khi gặp khó khăn.