Góc ngoài tam giác là một khái niệm quan trọng trong hình học, thường xuất hiện trong các bài toán liên quan đến tam giác. Hiểu rõ về góc ngoài tam giác giúp học sinh giải quyết các bài tập một cách nhanh chóng và chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu về góc ngoài tam giác, cùng với các bài tập thực hành đa dạng để bạn có thể nắm vững kiến thức này.
Góc ngoài tam giác là gì? Tính chất góc ngoài tam giác
Góc ngoài tam giác là góc kề bù với một góc trong tam giác.
Ví dụ:
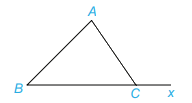
Góc ACx là góc ngoài tại C của tam giác ABC.
Tính chất:
Góc ngoài của một tam giác có số đo bằng tổng số đo của hai góc trong không kề với nó.
Trong hình học, góc ngoài của một tam giác là góc tạo bởi một cạnh của tam giác và đường thẳng kéo dài cạnh đối diện. Để hiểu rõ hơn, hãy xem xét tam giác ABC. Nếu kéo dài cạnh BC ra ngoài điểm C, ta được góc ACD. Góc ACD này được gọi là góc ngoài tại đỉnh C của tam giác ABC.
Tính chất quan trọng nhất của góc ngoài tam giác là:
Các bài tập về góc ngoài tam giác thường xoay quanh việc tính góc ngoài, tìm mối liên hệ giữa góc ngoài và các góc trong của tam giác, và ứng dụng tính chất của góc ngoài để giải quyết các bài toán phức tạp hơn.
Nếu bạn biết hai góc trong của một tam giác, bạn có thể dễ dàng tính góc ngoài tại đỉnh còn lại bằng cách sử dụng công thức: Góc ngoài = Tổng hai góc trong không kề.
Ví dụ: Cho tam giác ABC có góc A = 60 độ, góc B = 80 độ. Tính góc ngoài tại đỉnh C.
Giải:
Góc C = 180 độ - (góc A + góc B) = 180 độ - (60 độ + 80 độ) = 40 độ.
Góc ngoài tại đỉnh C = góc A + góc B = 60 độ + 80 độ = 140 độ.
Trong một số bài toán, bạn có thể cần tìm mối liên hệ giữa góc ngoài và các góc trong của tam giác để giải quyết bài toán. Ví dụ, bạn có thể cần chứng minh rằng một đường thẳng là phân giác của một góc.
Tính chất của góc ngoài tam giác có thể được ứng dụng để giải quyết nhiều bài toán hình học khác nhau. Ví dụ, bạn có thể sử dụng tính chất này để chứng minh rằng hai tam giác đồng dạng, hoặc để tính độ dài của một cạnh của tam giác.
Để củng cố kiến thức về góc ngoài tam giác, hãy thử giải các bài tập sau:
Góc ngoài tam giác còn có liên hệ mật thiết với các đường thẳng song song. Nếu một cạnh của tam giác song song với một đường thẳng, thì góc ngoài tại đỉnh đối diện sẽ bằng góc trong so le trong với đường thẳng đó.
Góc ngoài tam giác là một khái niệm cơ bản nhưng quan trọng trong hình học. Việc nắm vững định nghĩa, tính chất và các ứng dụng của góc ngoài tam giác sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của bạn.
| Khái niệm | Định nghĩa |
|---|---|
| Góc ngoài tam giác | Góc tạo bởi một cạnh của tam giác và đường thẳng kéo dài cạnh đối diện. |
| Tính chất | Góc ngoài tại một đỉnh bằng tổng hai góc trong không kề. |
| Nguồn: giaitoan.edu.vn | |