Định lí tổng 3 góc của tam giác là một trong những khái niệm cơ bản và quan trọng nhất trong hình học. Nó được áp dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác, từ đơn giản đến phức tạp.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để giúp bạn nắm vững định lí này một cách hiệu quả.
Tổng 3 góc của tam giác bằng bao nhiêu độ?
Tổng các góc của một tam giác bằng 180 độ.
Ví dụ:
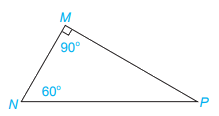
Xét tam giác MNP, có: \(\widehat M + \widehat N + \widehat P = 180^\circ \) (định lí tổng ba góc trong tam giác)
\(\begin{array}{l} \Rightarrow 90^\circ + 60^\circ + \widehat P = 180^\circ \\ \Rightarrow \widehat P = 180^\circ - 90^\circ - 60^\circ = 30^\circ \end{array}\)
Định lí tổng 3 góc của tam giác phát biểu rằng: Trong một tam giác, tổng số đo ba góc bằng 180 độ.
Có nhiều cách để chứng minh định lí này. Một trong những cách phổ biến nhất là sử dụng đường thẳng song song:
Xét tam giác ABC. Giả sử góc A = 60 độ, góc B = 80 độ. Khi đó, góc C = 180 độ - (60 độ + 80 độ) = 40 độ.
Định lí tổng 3 góc của tam giác có ứng dụng rộng rãi trong nhiều lĩnh vực, bao gồm:
Định lí tổng 3 góc của tam giác chỉ áp dụng cho tam giác trên mặt phẳng Euclid. Trong hình học phi Euclid, tổng ba góc của một tam giác có thể lớn hơn hoặc nhỏ hơn 180 độ.
Hãy giải các bài tập sau để củng cố kiến thức về định lí tổng 3 góc của tam giác:
Khi giải các bài toán liên quan đến định lí tổng 3 góc của tam giác, hãy chú ý đến đơn vị đo góc (độ hoặc radian) và đảm bảo rằng tổng số đo ba góc bằng 180 độ.
| Loại Tam Giác | Đặc Điểm |
|---|---|
| Tam giác nhọn | Ba góc đều nhỏ hơn 90 độ |
| Tam giác vuông | Một góc bằng 90 độ |
| Tam giác tù | Một góc lớn hơn 90 độ |
Hy vọng với những kiến thức và bài tập trên, bạn đã hiểu rõ hơn về định lí tổng 3 góc của tam giác. Hãy luyện tập thường xuyên để nắm vững kiến thức này và áp dụng vào giải các bài toán thực tế.