Trong chương trình học Toán lớp 7, việc nắm vững các trường hợp bằng nhau của tam giác là vô cùng quan trọng. Trường hợp bằng nhau thứ nhất, hay còn gọi là trường hợp cạnh - cạnh - cạnh (c.c.c), là nền tảng để giải quyết nhiều bài toán hình học.
Bài viết này sẽ cung cấp cho bạn kiến thức đầy đủ và chi tiết về trường hợp bằng nhau thứ nhất của tam giác, kèm theo các ví dụ minh họa và bài tập thực hành để bạn có thể hiểu rõ và áp dụng một cách hiệu quả.
Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c)
Nếu 3 cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Ví dụ:
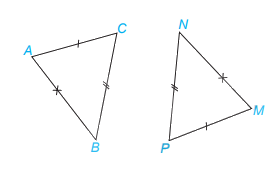
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Trong hình học, việc chứng minh hai tam giác bằng nhau là một kỹ năng cơ bản và quan trọng. Có nhiều cách để chứng minh hai tam giác bằng nhau, và một trong những cách phổ biến nhất là sử dụng trường hợp bằng nhau thứ nhất: cạnh – cạnh – cạnh (c.c.c).
Hai tam giác bằng nhau nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia. Ký hiệu:
Để chứng minh hai tam giác bằng nhau theo trường hợp c.c.c, ta cần chứng minh ba cạnh tương ứng của hai tam giác bằng nhau. Chứng minh này thường được thực hiện bằng cách sử dụng các tính chất của đoạn thẳng, góc và các định lý đã học.
Ví dụ 1: Cho tam giác ABC và tam giác DEF có AB = DE = 5cm, BC = EF = 7cm, CA = FD = 9cm. Chứng minh rằng ΔABC = ΔDEF.
Giải:
Ví dụ 2: Cho hình vẽ, biết AB = CD, BC = DA. Chứng minh rằng ΔABC = ΔCDA.
(Hình vẽ minh họa hai tam giác ABC và CDA có AB = CD, BC = DA, AC chung)
Giải:
Bài 1: Cho tam giác PQR và tam giác XYZ có PQ = XY = 3cm, QR = YZ = 4cm, RP = ZX = 5cm. Chứng minh rằng ΔPQR = ΔXYZ.
Bài 2: Cho hình vẽ, biết AM = BN, AB = MN. Chứng minh rằng ΔABM = ΔBNA.
(Hình vẽ minh họa hai tam giác ABM và BNA có AM = BN, AB = MN, BM chung)
Khi sử dụng trường hợp bằng nhau c.c.c, cần đảm bảo rằng ba cạnh tương ứng của hai tam giác bằng nhau. Thứ tự các cạnh không quan trọng, miễn là ba cạnh của tam giác này bằng ba cạnh của tam giác kia.
Trường hợp bằng nhau c.c.c được ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán chứng minh hai tam giác bằng nhau. Nó cũng là cơ sở để suy ra các tính chất khác của tam giác, như các góc bằng nhau, các đường cao bằng nhau, v.v.
Ngoài trường hợp bằng nhau c.c.c, còn có các trường hợp bằng nhau khác của tam giác, như cạnh – góc – cạnh (c.g.c), góc – cạnh – góc (g.c.g), góc – góc – cạnh (g.g.c). Việc nắm vững tất cả các trường hợp bằng nhau của tam giác sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả hơn.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c). Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng một cách thành thạo.