Trong chương trình học toán lớp 6 và lớp 7, khái niệm Hai góc kề bù đóng vai trò quan trọng trong việc hiểu về các mối quan hệ giữa các góc. Bài viết này trên giaitoan.edu.vn sẽ cung cấp kiến thức đầy đủ và dễ hiểu về định nghĩa, tính chất và cách áp dụng của hai góc kề bù.
Chúng ta sẽ cùng nhau khám phá những kiến thức cơ bản, các ví dụ minh họa và bài tập thực hành để bạn có thể tự tin giải quyết các bài toán liên quan đến chủ đề này.
2 góc kề bù là hai góc có một cạnh chung, 2 cạnh còn lại là hai tia đối nhau
Hai góc có một cạnh chung, 2 cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.
* Tính chất: 2 góc kề bù có tổng số đo là 180 độ.
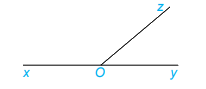
Góc xOz và góc yOz là 2 góc kề bù vì có tia Oz chung; tia Ox và Oy là 2 tia đối nhau.
Ta có: \(\widehat {xOz} + \widehat {yOz} = 180^\circ \)
Chú ý:
Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa 2 tia Ox và Oy. Khi đó:
\(\widehat {xOM} + \widehat {MOy} = \widehat {xOy}\)
Trong hình học, góc là một khái niệm cơ bản và quan trọng. Việc hiểu rõ các loại góc và mối quan hệ giữa chúng là nền tảng để giải quyết các bài toán phức tạp hơn. Một trong những khái niệm quan trọng đó là hai góc kề bù. Bài viết này sẽ cung cấp một cái nhìn toàn diện về hai góc kề bù, bao gồm định nghĩa, tính chất, cách nhận biết và ứng dụng trong giải toán.
Hai góc kề bù là hai góc có chung cạnh, không có điểm chung ngoài cạnh chung và tổng số đo của hai góc bằng 180 độ. Nói cách khác, hai góc kề bù tạo thành một góc bẹt.
Ví dụ: Giả sử có góc ∠AOB và ∠BOC có chung cạnh OB. Nếu ∠AOB + ∠BOC = 180°, thì ∠AOB và ∠BOC là hai góc kề bù.
Tính chất quan trọng nhất của hai góc kề bù là tổng số đo của chúng luôn bằng 180 độ. Điều này có nghĩa là nếu biết số đo của một góc trong cặp góc kề bù, ta có thể dễ dàng tính được số đo của góc còn lại.
Công thức: ∠AOB + ∠BOC = 180° (nếu ∠AOB và ∠BOC là hai góc kề bù)
Để nhận biết hai góc kề bù, ta cần kiểm tra hai điều kiện sau:
Hai góc kề bù được ứng dụng rộng rãi trong giải các bài toán liên quan đến góc, đặc biệt là trong các bài toán chứng minh, tính toán góc và xác định mối quan hệ giữa các góc.
Cho ∠ABC = 60°. Góc kề bù với ∠ABC có số đo là bao nhiêu?
Giải:
Gọi ∠CBD là góc kề bù với ∠ABC. Ta có:
∠ABC + ∠CBD = 180°
60° + ∠CBD = 180°
∠CBD = 180° - 60° = 120°
Vậy, góc kề bù với ∠ABC có số đo là 120°.
Hai góc kề bù có số đo hơn kém nhau 40°. Tính số đo của mỗi góc.
Giải:
Gọi số đo của góc lớn hơn là x, số đo của góc nhỏ hơn là x - 40°. Ta có:
x + (x - 40°) = 180°
2x - 40° = 180°
2x = 220°
x = 110°
Vậy, số đo của góc lớn hơn là 110° và số đo của góc nhỏ hơn là 110° - 40° = 70°.
Dưới đây là một số bài tập để bạn luyện tập và củng cố kiến thức về hai góc kề bù:
Hai góc kề bù là một khái niệm quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các góc. Việc nắm vững định nghĩa, tính chất và ứng dụng của hai góc kề bù là cần thiết để giải quyết các bài toán hình học một cách hiệu quả. Hy vọng bài viết này trên giaitoan.edu.vn đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học toán.