Sự đồng quy của ba đường trung trực của tam giác

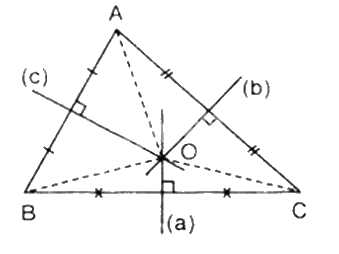
Trong hình học Euclid, đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó. Đối với một tam giác bất kỳ, ba đường trung trực của ba cạnh của tam giác đồng quy tại một điểm duy nhất. Điểm đồng quy này được gọi là tâm đường tròn ngoại tiếp của tam giác.

1. Định Nghĩa và Khái Niệm Cơ Bản

Đường trung trực của một cạnh của tam giác là đường thẳng vuông góc với cạnh đó tại trung điểm của cạnh đó. Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực. Đường tròn ngoại tiếp là đường tròn đi qua cả ba đỉnh của tam giác, và tâm của nó chính là tâm đường tròn ngoại tiếp.

2. Chứng Minh Sự Đồng Quy

Có nhiều cách để chứng minh sự đồng quy của ba đường trung trực. Một trong những cách phổ biến nhất là sử dụng tính chất của trung điểm và đường vuông góc.

1. Xét hai đường trung trực của hai cạnh AB và AC của tam giác ABC. Gọi giao điểm của chúng là O.
2. Vì O nằm trên đường trung trực của AB, nên OA = OB.
3. Tương tự, vì O nằm trên đường trung trực của AC, nên OA = OC.
4. Từ OA = OB và OA = OC, suy ra OB = OC.
5. Do đó, O nằm trên đường trung trực của BC.
6. Vậy, ba đường trung trực của tam giác ABC đồng quy tại O.

3. Tính Chất của Tâm Đường Tròn Ngoại Tiếp

• Tâm đường tròn ngoại tiếp cách đều ba đỉnh của tam giác.
• Bán kính của đường tròn ngoại tiếp (R) được tính theo công thức: R = (abc) / (4S), trong đó a, b, c là độ dài ba cạnh của tam giác và S là diện tích của tam giác.

4. Ứng Dụng của Sự Đồng Quy trong Giải Toán

Sự đồng quy của ba đường trung trực có nhiều ứng dụng trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến đường tròn ngoại tiếp.

Ví dụ 1: Xác định tâm đường tròn ngoại tiếp

Cho tam giác ABC. Hãy xác định tâm đường tròn ngoại tiếp của tam giác này bằng cách vẽ ba đường trung trực của ba cạnh và tìm giao điểm của chúng.

Ví dụ 2: Tính bán kính đường tròn ngoại tiếp

Cho tam giác ABC có AB = 3cm, BC = 4cm, AC = 5cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

Giải:

Tam giác ABC là tam giác vuông tại B (vì 3² + 4² = 5²). Do đó, tâm đường tròn ngoại tiếp nằm tại trung điểm của cạnh huyền AC.

Bán kính R = AC / 2 = 5 / 2 = 2.5cm.

5. Mối Quan Hệ Giữa Tâm Đường Tròn Ngoại Tiếp và Các Tâm Khác của Tam Giác

Tâm đường tròn ngoại tiếp là một trong bốn tâm đặc biệt của tam giác, bao gồm:

• Tâm đường tròn ngoại tiếp (O)
• Tâm đường tròn nội tiếp (I)
• Trọng tâm (G)
• Trực tâm (H)

Bốn điểm O, G, H, I này liên hệ với nhau bởi định lý Euler: OH² = 9R² - (a² + b² + c²).

6. Bài Tập Thực Hành

Dưới đây là một số bài tập để bạn luyện tập và củng cố kiến thức về sự đồng quy của ba đường trung trực:

1. Cho tam giác ABC, vẽ ba đường trung trực và xác định tâm đường tròn ngoại tiếp.
2. Cho tam giác ABC có AB = 5cm, BC = 7cm, AC = 8cm. Tính bán kính đường tròn ngoại tiếp.
3. Chứng minh rằng tâm đường tròn ngoại tiếp của tam giác đều là trọng tâm, trực tâm và tâm đường tròn nội tiếp.

7. Kết Luận

Sự đồng quy của ba đường trung trực là một tính chất quan trọng trong hình học, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong tam giác và ứng dụng vào việc giải các bài toán thực tế. Hy vọng bài viết này tại giaitoan.edu.vn đã cung cấp cho bạn những kiến thức hữu ích và đầy đủ về chủ đề này.