Chào mừng bạn đến với bài học về cộng, trừ hai đa thức một biến trên giaitoan.edu.vn. Đây là một trong những kiến thức cơ bản và quan trọng trong chương trình đại số, giúp bạn xây dựng nền tảng vững chắc cho các bài học nâng cao hơn.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, quy tắc, và các ví dụ minh họa để nắm vững phương pháp thực hiện các phép toán này một cách hiệu quả.
Cộng, trừ hai đa thức một biến
Cách 1:
Để cộng (hay trừ) hai đa thức, ta làm như sau:
Bước 1: Viết hai đa thức trong dấu ngoặc
Bước 2: Thực hiện bỏ dấu ngoặc (theo quy tắc dấu ngoặc)
Bước 3: Nhóm các hạng tử đồng dạng
Bước 4: Cộng, trừ các đơn thức đồng dạng.
Ví dụ: Cho đa thức \(P(x) = 3 + 5{x^2} - 3{x^3} + 4{x^2} - 2x - {x^3} + 5{x^5}.\) Thu gọn và sắp xếp đa thức \(P\left( x \right)\)
Giải
\(P(x) = 3 + 5{x^2} - 3{x^3} + 4{x^2} - 2x - {x^3} + 5{x^5}\)
\( = 5{x^5} + \left( { - 3{x^3} - {x^3}} \right) + \left( {5{x^2} + 4{x^2}} \right) - 2x + 3\)
\( = 5{x^5} - 4{x^3} + 9{x^2} - 2x + 3\)
Cách 2:
Đặt tính cộng sao cho các hạng tử cùng bậc đặt thẳng cột với nhau rồi cộng theo từng cột:
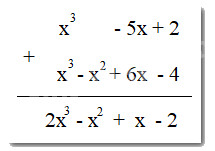
Chú ý: Nếu Q + R = P thì R = P – Q
Nếu R = P – Q thì Q + R = P
Trong đại số, đa thức là một biểu thức toán học bao gồm các số hạng được kết hợp với nhau bằng các phép cộng, trừ và nhân. Đa thức một biến là đa thức mà mỗi số hạng chỉ chứa một biến duy nhất, thường là 'x'. Việc cộng, trừ hai đa thức một biến là một kỹ năng cơ bản, cần thiết để giải quyết nhiều bài toán đại số phức tạp hơn.
Một đa thức một biến có dạng tổng quát:
P(x) = anxn + an-1xn-1 + ... + a1x + a0
Trong đó:
Để cộng hai đa thức một biến, ta thực hiện các bước sau:
Ví dụ:
P(x) = 3x2 + 2x - 1
Q(x) = -x2 + 5x + 4
P(x) + Q(x) = (3x2 - x2) + (2x + 5x) + (-1 + 4) = 2x2 + 7x + 3
Để trừ hai đa thức một biến, ta thực hiện các bước sau:
Ví dụ:
P(x) = 3x2 + 2x - 1
Q(x) = -x2 + 5x + 4
P(x) - Q(x) = 3x2 + 2x - 1 - (-x2 + 5x + 4) = 3x2 + 2x - 1 + x2 - 5x - 4 = 4x2 - 3x - 5
Ví dụ 1: Cộng hai đa thức sau:
A(x) = 5x3 - 2x2 + x - 7
B(x) = -3x3 + 4x2 - 5x + 2
A(x) + B(x) = (5x3 - 3x3) + (-2x2 + 4x2) + (x - 5x) + (-7 + 2) = 2x3 + 2x2 - 4x - 5
Ví dụ 2: Trừ hai đa thức sau:
C(x) = 2x2 - 3x + 1
D(x) = x2 + 2x - 4
C(x) - D(x) = 2x2 - 3x + 1 - (x2 + 2x - 4) = 2x2 - 3x + 1 - x2 - 2x + 4 = x2 - 5x + 5
Hãy thực hiện các phép cộng, trừ đa thức sau:
Cộng, trừ đa thức là một kỹ năng quan trọng trong nhiều lĩnh vực của toán học và khoa học, bao gồm:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về cách cộng, trừ hai đa thức một biến. Hãy luyện tập thường xuyên để nắm vững kỹ năng này và áp dụng vào giải quyết các bài toán đại số khác. Chúc bạn học tập tốt!