Trong hình học, sự đồng quy của ba đường cao trong một tam giác là một tính chất quan trọng và thường xuyên xuất hiện trong các bài toán. Bài viết này trên giaitoan.edu.vn sẽ cung cấp cho bạn kiến thức đầy đủ và dễ hiểu về khái niệm này.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, và cách chứng minh sự đồng quy của ba đường cao, cùng với các ví dụ minh họa cụ thể.
Sự đồng quy của ba đường cao của tam giác
Trong một tam giác, đoạn thẳng kẻ từ 1 đỉnh, vuông góc với cạnh đối diện gọi là đường cao của tam giác.
Định lí: Ba đường cao của một tam giác đồng quy tại 1 điểm.
Giao điểm của ba đường cao gọi là trực tâm của tam giác.
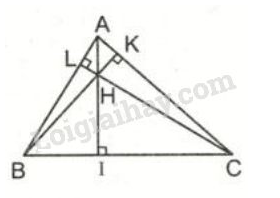
Chú ý: Trong tam giác cân tại A, đường cao kẻ từ đỉnh A đồng thời là đường trung tuyến, đường phân giác, đường trung trực của tam giác.
Trong hình học Euclid, đường cao của một tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh của tam giác xuống cạnh đối diện (hoặc đường kéo dài của cạnh đối diện). Ba đường cao của một tam giác đồng quy tại một điểm duy nhất, điểm này được gọi là trực tâm của tam giác. Đây là một trong những tính chất cơ bản và quan trọng của tam giác.
Đường cao của tam giác ABC, ký hiệu là AH (H thuộc BC), là đoạn thẳng vuông góc từ đỉnh A xuống cạnh BC. Tương tự, BH và CH là đường cao từ đỉnh B và C.
Trực tâm (H) của tam giác ABC là giao điểm của ba đường cao AH, BH, và CH.
Có nhiều cách để chứng minh sự đồng quy của ba đường cao. Một trong những cách phổ biến nhất là sử dụng tính chất của đường trung trực và đường phân giác.
Trực tâm H có nhiều tính chất quan trọng:
Trực tâm H cùng với trọng tâm G, tâm đường tròn ngoại tiếp O, và tâm đường tròn nội tiếp I tạo thành một hệ thống các điểm đặc biệt trong tam giác, được gọi là bốn tâm của tam giác. Các tâm này có mối quan hệ chặt chẽ với nhau, được thể hiện qua đường thẳng Euler.
Đường thẳng Euler là đường thẳng đi qua trọng tâm G, trực tâm H, và tâm đường tròn ngoại tiếp O. Đặc biệt, HG = 2OG.
Sự đồng quy của ba đường cao có nhiều ứng dụng trong việc giải toán hình học:
Bài tập 1: Cho tam giác ABC vuông tại A, với AB = 3cm, AC = 4cm. Tính độ dài đường cao AH.
Giải: Diện tích tam giác ABC là (1/2) * AB * AC = (1/2) * 3 * 4 = 6 cm2. Mặt khác, diện tích tam giác ABC cũng bằng (1/2) * BC * AH. Áp dụng định lý Pitago, BC = √(AB2 + AC2) = √(32 + 42) = 5cm. Vậy, AH = (2 * Diện tích) / BC = (2 * 6) / 5 = 2.4cm.
Bài tập 2: Cho tam giác ABC cân tại A. Gọi H là trực tâm của tam giác. Chứng minh rằng AH là đường phân giác của góc BAC.
Giải: Vì tam giác ABC cân tại A, đường cao từ A xuống BC cũng là đường trung tuyến và đường phân giác. Do đó, AH là đường phân giác của góc BAC.
Sự đồng quy của ba đường cao là một tính chất quan trọng và hữu ích trong hình học. Việc nắm vững định nghĩa, tính chất, và ứng dụng của nó sẽ giúp bạn giải quyết nhiều bài toán hình học một cách hiệu quả. Hy vọng bài viết này trên giaitoan.edu.vn đã cung cấp cho bạn những kiến thức cần thiết về chủ đề này.
| Khái niệm | Mô tả |
|---|---|
| Đường cao | Đoạn thẳng vuông góc từ đỉnh xuống cạnh đối diện |
| Trực tâm | Giao điểm của ba đường cao |
| Đường thẳng Euler | Đường thẳng đi qua trọng tâm, trực tâm và tâm đường tròn ngoại tiếp |