Trong hình học, tam giác là một trong những hình cơ bản và quan trọng nhất. Việc phân loại tam giác dựa trên số đo các góc là một kiến thức nền tảng cần nắm vững. Bài viết này sẽ cung cấp thông tin chi tiết về Tam giác nhọn, Tam giác vuông và Tam giác tù, giúp bạn hiểu rõ hơn về đặc điểm và tính chất của từng loại.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giảng, bài tập và tài liệu học tập chất lượng cao, giúp bạn nắm vững kiến thức về tam giác và các khái niệm hình học khác.
Tam giác nhọn, tam giác vuông, tam giác tù
+ Tam giác có ba góc đều nhọn gọi là tam giác nhọn
Ví dụ:
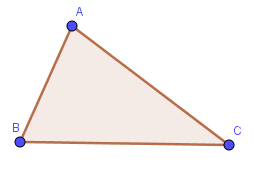
Tam giác ABC là tam giác nhọn vì cả 3 góc A, B, C trong tam giác đều là góc nhọn.
+ Tam giác có 1 góc tù gọi là tam giác tù
Ví dụ:
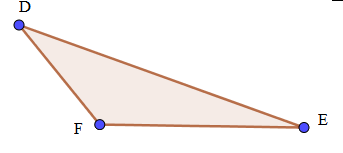
Tam giác DEF là tam giác nhọn vì góc F là góc tù (có số đo lớn hơn 90 độ)
+ Tam giác có 1 góc vuông gọi là tam giác vuông
Ví dụ:
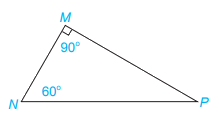
Tam giác MNP vuông tại M có: 2 cạnh MN và MP là 2 cạnh góc vuông, cạnh NP là cạnh huyền
Chú ý: 2 góc nhọn trong tam giác vuông có tổng số đo là 90 độ
Tam giác là hình hình học phẳng được tạo thành bởi ba đoạn thẳng gọi là cạnh, nối với nhau tại ba điểm gọi là đỉnh. Việc phân loại tam giác dựa trên số đo các góc trong tam giác là một phương pháp quan trọng trong hình học. Có ba loại tam giác chính: tam giác nhọn, tam giác vuông và tam giác tù.
Định nghĩa: Tam giác nhọn là tam giác mà cả ba góc đều nhỏ hơn 90 độ. Điều này có nghĩa là tất cả các góc trong tam giác đều là góc nhọn.
Tính chất:
Ví dụ: Một tam giác có các góc đo 60 độ, 70 độ và 50 độ là một tam giác nhọn.
Định nghĩa: Tam giác vuông là tam giác có một góc bằng 90 độ. Góc 90 độ này được gọi là góc vuông.
Tính chất:
Ví dụ: Một tam giác có các góc đo 90 độ, 30 độ và 60 độ là một tam giác vuông.
Định nghĩa: Tam giác tù là tam giác có một góc lớn hơn 90 độ. Góc lớn hơn 90 độ này được gọi là góc tù.
Tính chất:
Ví dụ: Một tam giác có các góc đo 100 độ, 40 độ và 40 độ là một tam giác tù.
Để phân biệt các loại tam giác này, bạn cần đo hoặc tính toán số đo của các góc trong tam giác. Dưới đây là bảng tóm tắt:
| Loại Tam Giác | Số Đo Các Góc |
|---|---|
| Tam Giác Nhọn | Tất cả các góc đều nhỏ hơn 90 độ |
| Tam Giác Vuông | Một góc bằng 90 độ |
| Tam Giác Tù | Một góc lớn hơn 90 độ |
Việc phân loại tam giác có nhiều ứng dụng trong thực tế và trong các lĩnh vực khác của toán học, chẳng hạn như:
Hiểu rõ về Tam giác nhọn, Tam giác vuông và Tam giác tù là nền tảng quan trọng trong học toán hình học. Việc nắm vững các định nghĩa, tính chất và ứng dụng của từng loại tam giác sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và chính xác hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.