Trong chương trình học Toán lớp 7, 8, 9, kiến thức về tam giác vuông và các trường hợp bằng nhau của tam giác là vô cùng quan trọng. Trường hợp bằng nhau cạnh huyền – góc nhọn là một trong những trường hợp đặc biệt giúp chúng ta xác định hai tam giác vuông có bằng nhau hay không.
Bài viết này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về trường hợp bằng nhau cạnh huyền – góc nhọn, cùng với các ví dụ minh họa và bài tập thực hành để bạn có thể nắm vững kiến thức này.
Trường hợp bằng nhau cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( cạnh huyền – góc nhọn)
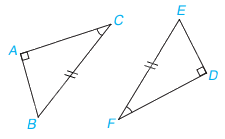
Xét tam giác vuông ABC và DEF, ta có:
BC = EF
\(\widehat C = \widehat F\)
Vậy \(\Delta ABC = \Delta DEF\) (cạnh huyền – góc nhọn)
Trong hình học, hai tam giác vuông được gọi là bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau. Tuy nhiên, việc chứng minh tất cả các cạnh và góc bằng nhau có thể tốn nhiều thời gian. Do đó, người ta đã tìm ra các trường hợp bằng nhau của tam giác vuông, trong đó có trường hợp bằng nhau cạnh huyền – góc nhọn.
Định nghĩa: Hai tam giác vuông bằng nhau nếu chúng có một cạnh huyền và một góc nhọn tương ứng bằng nhau.
Điều kiện: Cho hai tam giác vuông ABC và A'B'C' vuông tại A và A' tương ứng. Nếu:
Thì ΔABC = ΔA'B'C' (cạnh huyền – góc nhọn).
Để chứng minh trường hợp bằng nhau cạnh huyền – góc nhọn, ta có thể sử dụng các kiến thức về tổng các góc trong một tam giác và các tính chất của tam giác vuông.
Chứng minh:
Ví dụ 1: Cho tam giác ABC vuông tại A, AB = 3cm, BC = 5cm. Cho tam giác A'B'C' vuông tại A', B'C' = 5cm, ∠B' = ∠B. Chứng minh ΔABC = ΔA'B'C'.
Giải:
Xét ΔABC và ΔA'B'C':
Vậy, ΔABC = ΔA'B'C' (cạnh huyền – góc nhọn).
Ví dụ 2: Cho tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A'. Biết AB = A'B' = 4cm và AC = A'C' = 3cm. Chứng minh ΔABC = ΔA'B'C'.
Giải:
Áp dụng định lý Pytago vào tam giác ABC, ta có:
BC2 = AB2 + AC2 = 42 + 32 = 16 + 9 = 25
Suy ra BC = 5cm.
Tương tự, áp dụng định lý Pytago vào tam giác A'B'C', ta có:
B'C'2 = A'B'2 + A'C'2 = 42 + 32 = 16 + 9 = 25
Suy ra B'C' = 5cm.
Xét ΔABC và ΔA'B'C':
Vậy, ΔABC = ΔA'B'C' (cạnh huyền – cạnh góc vuông).
1. Cho tam giác ABC vuông tại A, AB = 5cm, BC = 13cm. Cho tam giác A'B'C' vuông tại A', B'C' = 13cm, ∠B' = ∠B. Chứng minh ΔABC = ΔA'B'C'.
2. Cho tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A'. Biết AB = A'B' = 6cm và ∠B = ∠B'. Chứng minh ΔABC = ΔA'B'C'.
3. Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm. Cho tam giác DEF vuông tại D, DE = 8cm, DF = 6cm. Chứng minh ΔABC = ΔDEF.
Trường hợp bằng nhau cạnh huyền – góc nhọn được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác vuông, đặc biệt là trong việc chứng minh hai tam giác vuông bằng nhau. Nó giúp đơn giản hóa quá trình chứng minh và tiết kiệm thời gian.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức đầy đủ và chi tiết về trường hợp bằng nhau cạnh huyền – góc nhọn. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức này và áp dụng vào giải các bài toán thực tế.