Trong chương trình học toán lớp 7, 8, 9, việc nắm vững các trường hợp bằng nhau của tam giác vuông là vô cùng quan trọng. Trường hợp bằng nhau cạnh huyền – cạnh góc vuông là một trong những trường hợp cơ bản và thường xuyên xuất hiện trong các bài toán. Bài viết này sẽ cung cấp kiến thức đầy đủ và chi tiết về trường hợp này, giúp bạn hiểu rõ và áp dụng hiệu quả.
Chúng ta sẽ cùng tìm hiểu về điều kiện để hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông, cách chứng minh và ứng dụng của trường hợp này trong giải toán.
Trường hợp bằng nhau cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( cạnh huyền – cạnh góc vuông)
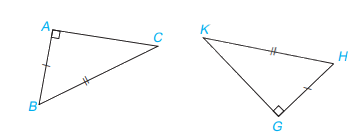
Xét tam giác vuông ABC và GHK, ta có:
BC = HK
AB = GH
Vậy \(\Delta ABC = \Delta GHK\) ( cạnh huyền – cạnh góc vuông)
Trong hình học, việc xác định sự bằng nhau của hai tam giác là một bài toán cơ bản. Có nhiều trường hợp để chứng minh hai tam giác bằng nhau, và một trong số đó là trường hợp bằng nhau cạnh huyền – cạnh góc vuông. Trường hợp này áp dụng cho hai tam giác vuông và dựa trên việc so sánh độ dài cạnh huyền và một cạnh góc vuông tương ứng.
Hai tam giác vuông bằng nhau khi và chỉ khi chúng có:
Ký hiệu: Nếu tam giác ABC vuông tại A và tam giác DEF vuông tại D, ta có: △ABC = △DEF ⇔ BC = EF và AB = DE (hoặc AC = DF)
Để chứng minh hai tam giác vuông bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông, ta cần chứng minh hai điều kiện trên. Thông thường, bài toán sẽ cho sẵn hoặc yêu cầu ta chứng minh hai điều kiện này.
Ví dụ 1: Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D. Biết BC = EF = 5cm và AB = DE = 3cm. Chứng minh △ABC = △DEF.
Giải:
Ví dụ 2: Cho tam giác PQR vuông tại Q và tam giác XYZ vuông tại Y. Biết PR = XZ = 10cm và PQ = XY = 6cm. Chứng minh △PQR = △XYZ.
Giải:
Trường hợp bằng nhau cạnh huyền – cạnh góc vuông được ứng dụng rộng rãi trong việc giải các bài toán liên quan đến tam giác vuông, đặc biệt là:
Để nắm vững kiến thức về trường hợp bằng nhau cạnh huyền – cạnh góc vuông, bạn nên luyện tập thêm các bài tập sau:
Khi áp dụng trường hợp bằng nhau cạnh huyền – cạnh góc vuông, cần đảm bảo rằng hai tam giác đang xét đều là tam giác vuông. Ngoài ra, cần chú ý đến thứ tự của các cạnh khi so sánh. Ví dụ, nếu AB = DE thì phải so sánh với DE, không phải với EF.
Ngoài trường hợp bằng nhau cạnh huyền – cạnh góc vuông, còn có các trường hợp bằng nhau khác của tam giác vuông, như trường hợp cạnh góc vuông – cạnh góc vuông và trường hợp góc nhọn – cạnh đối diện. Việc nắm vững tất cả các trường hợp này sẽ giúp bạn giải quyết các bài toán hình học một cách hiệu quả hơn.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về trường hợp bằng nhau cạnh huyền – cạnh góc vuông. Chúc bạn học tốt!