Bài học này sẽ hướng dẫn bạn cách thực hiện phép chia đa thức cho đa thức, tập trung vào trường hợp chia hết. Đây là một kỹ năng quan trọng trong đại số, giúp bạn giải quyết nhiều bài toán phức tạp hơn.
Chúng ta sẽ cùng nhau tìm hiểu các bước thực hiện, các ví dụ minh họa và các lưu ý quan trọng để bạn có thể nắm vững kiến thức này.
Chia đa thức cho đa thức, trường hợp chia hết
Đặt tính chia:
Bước 1: Đặt tính chia tương tự chia hai số tự nhiên. Lấy hạng tử bậc cao nhất của A chia cho hạng tử bậc cao nhất của B.
Bước 2: Lấy A trừ đi tích của B với thương ở bước 1, được dư thứ nhất.
Bước 3: Lấy hạng tử bậc cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B.
Bước 4: Lấy dư thứ nhất trừ đi tích của B với thương ở bước 3, ta thu được dư thứ 2.
Bước 5: Làm tương tự như trên, đến khi dư bằng 0 thì kết thúc.
Ví dụ:
Tính \(\left(2x^4 - x^3 + 2x - 1\right) : \(left( x^2 - x + 1\right)
- Lấy \(2x^4 : x^2\) được \(2x^2\), ta viết \(2x^2\) vào thương. Sau đó nhân lần lượt \(2x^2\) với các hạng tử của đa thức chia, ta được \(2x^4 - 2x^3 + 2x^2\). Lấy đa thức bị chia trừ đi đa thức \(2x^4 - 2x^3 + 2x^2\), được \(x^3 - 2x^2 + 2x - 1\).
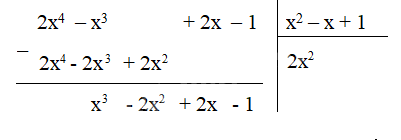
- Lấy \(x^3 : x^2\) được \(x\), ta viết \(+ x\) vào thương. Sau đó nhân lần lượt \(x\) với các hạng tử của đa thức chia, ta được \(x^3 - x^2 + x\). Lấy đa thức \(x^3 - 2x^2 + 2x - 1\) trừ đi đa thức \(x^3 - x^2 + x\), được \(-x^2 + x - 1\).
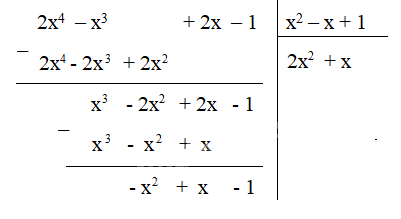
- Lấy \(-x^2 : x^2\) được \(-1\), ta viết \(-1\) vào thương. Sau đó nhân lần lượt \(-1\) với các hạng tử của đa thức chia, ta được \(-x^2 + x - 1\). Lấy đa thức \(-x^2 + x - 1\) trừ đi đa thức \(-x^2 + x - 1\), được \(0\).
Vậy \(\left(2x^4 - x^3 + 2x - 1\right) : \left( x^2 - x + 1\right) = 2x^2 + x - 1\)
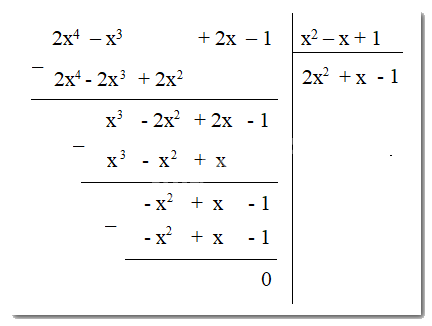
Trong toán học, đặc biệt là đại số, phép chia đa thức là một kỹ năng cơ bản và quan trọng. Bài viết này sẽ đi sâu vào phương pháp chia đa thức cho đa thức, tập trung vào trường hợp chia hết, cung cấp kiến thức nền tảng, các bước thực hiện chi tiết, ví dụ minh họa và bài tập thực hành để giúp bạn nắm vững kiến thức này.
Trước khi đi vào phương pháp chia đa thức, chúng ta cần ôn lại một số khái niệm cơ bản:
Phép chia đa thức cho đa thức tương tự như phép chia số thông thường, nhưng thay vì chia các chữ số, chúng ta chia các hạng tử của đa thức. Dưới đây là các bước thực hiện:
Ví dụ 1: Chia đa thức (2x2 + 5x + 3) cho đa thức (x + 1)
| Bước | Thực hiện | Kết quả |
|---|---|---|
| 1 | Chia 2x2 cho x | 2x |
| 2 | Nhân 2x với (x + 1) | 2x2 + 2x |
| 3 | Trừ (2x2 + 2x) từ (2x2 + 5x + 3) | 3x + 3 |
| 4 | Chia 3x cho x | 3 |
| 5 | Nhân 3 với (x + 1) | 3x + 3 |
| 6 | Trừ (3x + 3) từ (3x + 3) | 0 |
Vậy, (2x2 + 5x + 3) chia cho (x + 1) được thương là 2x + 3 và số dư là 0.
Ví dụ 2: Chia đa thức (x3 - 3x2 + 2x) cho đa thức (x - 1)
(Thực hiện tương tự như ví dụ 1)
Nếu sau khi thực hiện các bước chia, đa thức còn lại có bậc lớn hơn hoặc bằng bậc của đa thức chia, thì phép chia không hết. Khi đó, đa thức còn lại chính là số dư.
Phép chia đa thức cho đa thức là một kỹ năng quan trọng trong đại số. Việc nắm vững phương pháp chia đa thức, đặc biệt là trường hợp chia hết, sẽ giúp bạn giải quyết nhiều bài toán phức tạp hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng của mình.