Trong chương trình toán học, lũy thừa với số mũ tự nhiên là một khái niệm cơ bản nhưng vô cùng quan trọng. Nó giúp chúng ta biểu diễn các phép toán nhân lặp đi lặp lại một cách ngắn gọn và hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp các bài học chi tiết, dễ hiểu về lũy thừa với số mũ tự nhiên, phù hợp với học sinh lớp 6, lớp 7 và những ai muốn ôn lại kiến thức toán học.
Lũy thừa bậc n của một số hữu tỉ x
Lũy thừa bậc n của một số hữu tỉ x , kí hiệu xn , là tích của n thừa số x ( n là số tự nhiên lớn hợn 1)
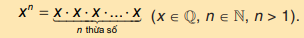
xn đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.
x: cơ số
n: số mũ
Quy ước: x0 = 1 ( x \( \ne \)0); x1 = x
Ví dụ: \((\dfrac{1}{2})^3 = \dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{8}\)
Chú ý:
\(\begin{array}{l}{(x.y)^n} = {x^n}.{y^n}\\{(\dfrac{x}{y})^n} = \dfrac{{{x^n}}}{{{y^n}}}\end{array}\)
+ Lũy thừa số mũ chẵn của 1 số hữu tỉ luôn dương
+ Lũy thừa số mũ lẻ của 1 số hữu tỉ âm luôn âm
Lũy thừa với số mũ tự nhiên là một phép toán toán học cơ bản, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hiểu rõ về lũy thừa là nền tảng quan trọng để học các khái niệm toán học nâng cao hơn.
Lũy thừa của một số a (gọi là cơ số) với số mũ tự nhiên n (khác 0) là tích của n thừa số bằng a. Ký hiệu là an.
Ví dụ: 23 = 2 * 2 * 2 = 8
Trong đó:
Có một số tính chất quan trọng của lũy thừa mà bạn cần nắm vững:
Hãy cùng xem xét một số ví dụ để hiểu rõ hơn về lũy thừa:
Để củng cố kiến thức về lũy thừa, hãy thử giải các bài tập sau:
Lũy thừa có rất nhiều ứng dụng trong thực tế, ví dụ:
Trong lập trình, lũy thừa thường được sử dụng để tính toán các giá trị phức tạp. Hầu hết các ngôn ngữ lập trình đều cung cấp các hàm hoặc toán tử để tính lũy thừa một cách dễ dàng.
Lũy thừa với số mũ tự nhiên là một khái niệm toán học quan trọng và có nhiều ứng dụng thực tế. Việc nắm vững kiến thức về lũy thừa sẽ giúp bạn giải quyết các bài toán toán học một cách hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng của mình.