Bài 1.15 trang 22 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải khác nhau để bạn có thể nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết và các kiến thức liên quan ngay sau đây!
Một cuộc thi gồm hai loại câu hỏi. Câu hỏi loại 1 và câu hỏi loại 2. Ở vòng 1 thí sinh bốc ngẫu nhiên câu hỏi loại (i in left{ {1;{rm{ }}2} right}). Nếu trả lời sai thì thí sinh dừng cuộc thi tại đây. Nếu trả lời đúng, thí sinh sẽ đi tiếp vào vòng 2, tiếp tục bốc ngẫu nhiên một câu hỏi loại (j in left{ {1;{rm{ }}2} right}(j ne i).) Sau khi thí sinh trả lời câu hỏi này, cuộc thi kết thúc. Thí sinh sẽ nhận được ({V_i}) điểm nếu trả lời đúng câu hỏi loại (i in left{ {1;{rm{
Đề bài
Một cuộc thi gồm hai loại câu hỏi. Câu hỏi loại 1 và câu hỏi loại 2. Ở vòng 1 thí sinh bốc ngẫu nhiên câu hỏi loại \(i \in \left\{ {1;{\rm{ }}2} \right\}\). Nếu trả lời sai thì thí sinh dừng cuộc thi tại đây. Nếu trả lời đúng, thí sinh sẽ đi tiếp vào vòng 2, tiếp tục bốc ngẫu nhiên một câu hỏi loại \(j \in \left\{ {1;{\rm{ }}2} \right\}(j \ne i).\) Sau khi thí sinh trả lời câu hỏi này, cuộc thi kết thúc. Thí sinh sẽ nhận được \({V_i}\) điểm nếu trả lời đúng câu hỏi loại \(i \in \left\{ {1;{\rm{ }}2} \right\}\). Giả thiết rằng việc trả lời đúng câu hỏi vòng 1 sẽ không ảnh hưởng đến xác suất trả lời đúng hay sai câu hỏi ở vòng 2. Bạn An tham gia cuộc thi. Gọi \({E_i}\) là biển cố: "An trả lời đúng câu hỏi loại \(i\)”(\(i \in \left\{ {1;{\rm{ }}2} \right\}\)). Giả sử \(P(E) = {p_i}\).
a) Với điều kiện nào thì ở vòng 1, An nên bốc ngẫu nhiên câu hỏi loại 1?
b) Giả sử \({p_1} = 0,6;{p_2} = 0,8;{V_1} = 20;{V_2} = 10\). Khi đó ở vòng 1, An nên bắc ngẫu nhiên câu hỏi loại nào?
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của biến ngẫu nhiên rời rạc, công thức nhân xác suất của 2 biến cố độc lập.
Lời giải chi tiết
Trường hợp 1: Nếu ở vòng 1 An bốc ngẫu nhiên câu hỏi loại 1.
+ Nếu trả lời sai thì An được 0 điểm. Cuộc thi kết thúc tại đây.
Vậy \(P({X_1} = 0) = P(\overline {{E_1}} ) = 1 - {p_1}.\)
+ Nếu trả lời đúng thì An nhận \({V_1}\) điểm và An được đi tiếp vòng 2: Bốc ngẫu nhiên một câu hỏi loại 2.
\({E_i}\) là biến cố: “Trả lời đúng câu hỏi loại \(i\)”, \(i \in \left\{ {1;2} \right\}\).
Nếu trả lời sai câu hỏi loại 2 thì An nhận 0 điểm. Cuộc thi kết thúc và An nhận được \({V_1}\) điểm.
Theo giả thiết \({E_1},\overline {{E_2}} \) là hai biến cố độc lập. Theo công thức nhân xác suất ta có:
\(P({X_1} = {V_1}) = P({E_1}\overline {{E_2}} ) = P({E_1}).P(\overline {{E_2}} ) = {p_1}(1 - {p_2})\)
Nếu trả lời đúng câu hỏi loại 2 thì An nhận \({V_2}\) điểm. Cuộc thi kết thúc và An nhận được \({V_1} + {V_2}\) điểm.
Theo giả thiết \({E_1},{E_2}\) là hai biến cố độc lập. Theo công thức nhân xác suất ta có:
\(P({X_1} = {V_1} + {V_2}) = P({E_1}{E_2}) = P({E_1}).P({E_2}) = {p_1}{p_2}\)
Ta có bảng phân bố xác suất của \({X_1}\) là:
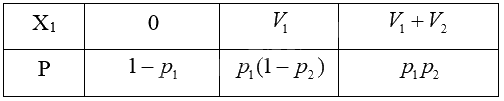
\(E({X_1}) = {V_1}{p_1}(1 - {p_2}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2}\)
Trường hợp 2: Nếu ở vòng 1 An bốc ngẫu nhiên câu hỏi loại 2.
Tương tự trường hợp 1, ta có bảng phân bố xác suất của \({X_2}\) là:
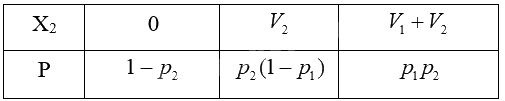
\(E({X_2}) = {V_2}{p_2}(1 - {p_1}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2}\)
a) Ở vòng 1 An nên chọn câu hỏi loại 1 trước nếu:
\(\begin{array}{l}E({X_1}) \ge E({X_2}) \Leftrightarrow {V_1}{p_1}(1 - {p_2}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2} > {V_2}{p_2}(1 - {p_1}) + \left( {{V_1} + {V_2}} \right){p_1}{p_2}\\{\rm{ }} \Leftrightarrow {V_1}{p_1}(1 - {p_2}) \ge {V_2}{p_2}(1 - {p_1})\\{\rm{ }} \Leftrightarrow \frac{{{V_1}{p_1}}}{{1 - {p_1}}} \ge \frac{{{V_2}{p_2}}}{{1 - {p_2}}}\end{array}\)
b) Ta có: \(\frac{{{V_1}{p_1}}}{{1 - {p_1}}} = \frac{{20.0,6}}{{1 - 0,6}} = 30;\frac{{{V_2}{p_2}}}{{1 - {p_2}}} = \frac{{10.0,8}}{{1 - 0,8}} = 40\)
Ta thấy \(\frac{{{V_1}{p_1}}}{{1 - {p_1}}} < \frac{{{V_2}{p_2}}}{{1 - {p_2}}}\)nên ở vòng 1 An nên chọn câu hỏi loại 2 trước.
Bài 1.15 trang 22 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2 và thực hiện các yêu cầu sau:
1. Xác định khoảng đơn điệu của hàm số:
Để xác định khoảng đơn điệu, ta cần tìm đạo hàm f'(x) và xét dấu của nó.
f'(x) = 3x2 - 6x = 3x(x - 2)
f'(x) = 0 khi x = 0 hoặc x = 2.
Ta lập bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Vậy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
2. Tìm cực trị của hàm số:
Dựa vào bảng xét dấu f'(x), ta thấy:
Vậy hàm số đạt cực đại tại điểm (0; 2) và cực tiểu tại điểm (2; -2).
3. Vẽ đồ thị hàm số:
Để vẽ đồ thị hàm số, ta cần xác định:
Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số f(x) = x3 - 3x2 + 2.
Trong quá trình giải bài tập, cần nắm vững các kiến thức về đạo hàm, khoảng đơn điệu, cực trị và cách vẽ đồ thị hàm số. Việc hiểu rõ các khái niệm này sẽ giúp bạn giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả.
Ngoài ra, bạn có thể tham khảo thêm các tài liệu học tập, sách giáo khoa và các trang web học toán online uy tín để nâng cao kiến thức và kỹ năng của mình.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!