Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn cách giải bài 2.9 trang 43 thuộc Chuyên đề học tập Toán 12 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích (5{rm{ }}l). Giá sản xuất mặt xung quanh là 100 nghìn đồng/m2, giá sản xuất mặt đáy là 120 nghìn đồng/m2. Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn? (Giả sử chi phí cho các mối nối không đáng kể)
Đề bài
Một công ty dự kiến chi 1 tỉ đồng sản xuất các thùng đựng sơn hình trụ với dung tích \(5{\rm{ }}l\). Giá sản xuất mặt xung quanh là 100 nghìn đồng/m2, giá sản xuất mặt đáy là 120 nghìn đồng/m2. Hỏi công ty có thể sản xuất được tối đa bao nhiêu thùng sơn (giả sử chi phí cho các mối nối không đáng kể)?
Phương pháp giải - Xem chi tiết
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết
Đổi: 5 lít = 5 \(d{m^3}\) = 0,005 \({m^3}\).
Gọi r (m) là bán kính của đáy thùng đựng sơn hình trụ, r > 0.
h (m) là chiều cao thùng sơn hình trụ, h > 0.
Ta có \({V_{tru}} = \pi {r^2}h \Leftrightarrow 0,005 = \pi {r^2}h \Leftrightarrow h = \frac{{0,005}}{{\pi {r^2}}}\) (m).
Diện tích xung quanh thùng sơn là: \({S_{xq}} = 2\pi rh = 2\pi r.\frac{{0,005}}{{\pi {r^2}}} = \frac{{0,01}}{r}\) \(\left( {{m^2}} \right)\).
Diện tích đáy thùng sơn là: \({S_{day}} = \pi {r^2}\) \(\left( {{m^2}} \right)\).
Giá sản xuất mặt xung quanh của một thùng sơn là:
\(100{S_{xq}} = 100.\frac{{0,01}}{r} = \frac{1}{r}\) (nghìn đồng).
Giá sản xuất mặt hai mặt đáy của một thùng sơn là:
\(120.2.\pi {r^2} = 240\pi {r^2}\) (nghìn đồng).
Chi phí sản xuất một thùng sơn là:
\(C(r) = \frac{1}{r} + 240\pi {r^2}\) (nghìn đồng).
Xét \(C'(r) = - \frac{1}{{{r^2}}} + 480\pi r = 0 \Leftrightarrow 480\pi r = \frac{1}{{{r^2}}} \Leftrightarrow 480\pi {r^3} = 1 \Leftrightarrow r = \sqrt[3]{{\frac{1}{{480\pi }}}}\).
Bảng biến thiên của hàm số C(r) trên \(\left( {0; + \infty } \right)\):
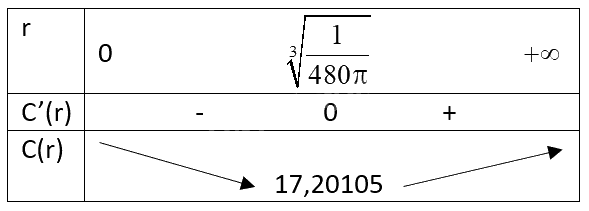
Từ bảng biến thiên, ta thấy giá trị nhỏ nhất của C(r) là xấp xỉ 17,20105 nghìn đồng.
Ta có \(\frac{{1000000}}{{17,20105}} \approx 58135,98533\).
Vậy công ty có thể sản xuất được tối đa 58135 thùng sơn.
Bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài toán này thường yêu cầu học sinh phân tích hàm số, tìm điểm cực trị, và xác định khoảng đồng biến, nghịch biến của hàm số.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Thông thường, đề bài sẽ yêu cầu tìm giá trị của một biểu thức, chứng minh một đẳng thức, hoặc giải một phương trình. Việc phân tích đề bài giúp chúng ta xác định được phương pháp giải phù hợp.
Đạo hàm là công cụ quan trọng để giải quyết bài toán này. Chúng ta cần tính đạo hàm của hàm số, tìm các điểm mà đạo hàm bằng 0 hoặc không xác định. Các điểm này có thể là điểm cực trị hoặc điểm không xác định của hàm số.
Sau khi tìm được đạo hàm, chúng ta có thể xác định khoảng đồng biến, nghịch biến của hàm số bằng cách xét dấu đạo hàm. Nếu đạo hàm dương trên một khoảng, hàm số đồng biến trên khoảng đó. Nếu đạo hàm âm trên một khoảng, hàm số nghịch biến trên khoảng đó.
Giả sử đề bài yêu cầu tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = x^3 - 3x^2 + 2 trên đoạn [-1; 3].
Ngoài việc giải bài tập, bạn nên tìm hiểu thêm về các ứng dụng của đạo hàm trong thực tế, như tìm điểm tối ưu trong kinh tế, vật lý, và kỹ thuật. Việc mở rộng kiến thức giúp bạn hiểu sâu hơn về môn Toán và ứng dụng nó vào cuộc sống.
Bài 2.9 trang 43 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp bạn rèn luyện kỹ năng về đạo hàm và ứng dụng của nó. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải quyết bài toán một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi tức thời của hàm số. |
| Điểm cực trị | Điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất. |
| Khoảng đồng biến | Khoảng mà hàm số tăng dần. |
| Khoảng nghịch biến | Khoảng mà hàm số giảm dần. |