Bài 2.15 trang 45 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải khác nhau để bạn có thể nắm vững kiến thức và tự tin giải các bài toán tương tự.
Hãy cùng khám phá lời giải chi tiết và các kiến thức liên quan ngay sau đây!
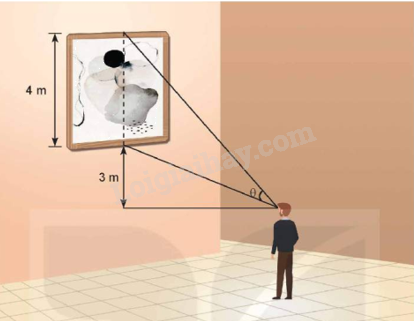
Một bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát là 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi (tức là, có góc nhìn \(\theta \) lớn nhất)?
Đề bài
Một bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát là 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi (tức là, có góc nhìn \(\theta \) lớn nhất)?
Phương pháp giải - Xem chi tiết
Sử dụng đạo hàm để giải quyết bài toán tối ưu.
Lời giải chi tiết
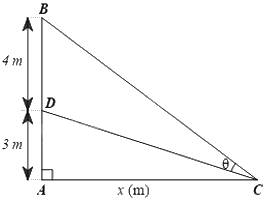
Đặt AC = x (m) ta có \(CD = \sqrt {{x^2} + 9} \), \(BC = \sqrt {{x^2} + 49} \)
Ta có: \(\sin B = \frac{x}{{\sqrt {{x^2} + 49} }}\)
Xét tam giác BDC có:
\(\frac{{CD}}{{\sin B}} = \frac{{BD}}{{\sin \theta }} \Leftrightarrow \frac{{\sqrt {{x^2} + 9} }}{{\frac{x}{{\sqrt {{x^2} + 49} }}}} = \frac{4}{{\sin \theta }} \Leftrightarrow \sin \theta = \frac{{4x}}{{\sqrt {{x^2} + 49} .\sqrt {{x^2} + 9} }}\)
Để có được tầm nhìn thuận lợi thì góc nhìn \(\theta \) lớn nhất.
Xét hàm số \(y = \frac{{4x}}{{\sqrt {{x^2} + 49} .\sqrt {{x^2} + 9} }} = \frac{{4x}}{{\sqrt {{x^4} + 58{x^2} + 441} }},x > 0\)
Ta có: \(y' = \frac{{ - 4{x^4} + 1764}}{{\left( {{x^4} + 58{x^2} + 441} \right)\sqrt {{x^4} + 58{x^2} + 441} }} = 0 \Leftrightarrow x = \sqrt {21} \approx 4,58\)
Vậy người đó phải đứng cách tường khoảng 4,58m thì tầm nhìn là thuận lợi nhất.
Bài 2.15 trang 45 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tối ưu hóa. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
(Nội dung lời giải chi tiết bài toán sẽ được trình bày tại đây, bao gồm các bước giải cụ thể, các phép tính và giải thích rõ ràng. Ví dụ:)
Đề bài: (Giả sử đề bài là tìm kích thước của một hình hộp chữ nhật có thể tích cho trước sao cho diện tích toàn phần nhỏ nhất)
Lời giải:
Ngoài bài 2.15, Chuyên đề học tập Toán 12 - Kết nối tri thức còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán tối ưu hóa. Để làm tốt các bài tập này, bạn cần:
Dưới đây là một số bài tập tương tự để bạn luyện tập:
Để học tập và ôn luyện kiến thức về đạo hàm và ứng dụng của đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 2.15 trang 45 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các hướng dẫn trên, bạn đã nắm vững kiến thức và tự tin giải các bài toán tương tự.