Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Chúng tôi xin giới thiệu bộ giải chi tiết các bài tập trong mục 1 của Chuyên đề học tập Toán 12 - Kết nối tri thức, bao gồm các trang 6, 7, 8 và 9.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán khó.
Gieo một con xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi (X)là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó a) Các giá trị có thể của (X) là gì? b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được (X) sẽ nhận giá trị nào không?
Trả lời câu hỏi Hoạt động 1 trang 6 Chuyên đề học tập Toán 12 Kết nối tri thức
Gieo một con xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi \(X\)là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó
a) Các giá trị có thể của \(X\) là gì?
b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được \(X\) sẽ nhận giá trị nào không?
Phương pháp giải:
Dựa vào thực nghiệm gieo một con xúc xắc 6 lần
Lời giải chi tiết:
a) \(X \in \left\{ {0;1;2;3;4;5;6} \right\}\).
b) Ta không thể khẳng định trước được.
Trả lời câu hỏi Luyện tập 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên đồng thời 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X.
Phương pháp giải:
Bước 1: Liệt kê các giá trị có thể của X
Bước 2: Tính các xác suất để X nhận các giá trị đó
Bước 3: Lập bảng phân bố xác suất cho biến ngẫu nhiên X
Lời giải chi tiết:
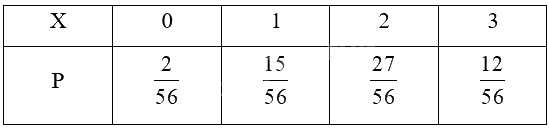
Các giá trị của X có thể nhận được thuộc tập {0; 1; 2; 3}.
Số kết quả có thể là \(C_{16}^3 = 560.\)
+ Biến cố \(\left\{ {X = 0} \right\}\) là: “Không có HS nam nào trong 3 HS được chọn”
Số cách chọn 3 học sinh nữ: \(C_6^3 = 20\) (cách chọn)
Do đó, \(P\left( {X = 0} \right)\; = \frac{{20}}{{560}} = \frac{2}{{56}}\)
+ Biến cố \(\left\{ {X = 1} \right\}\) là: “Chọn được 1 học sinh nam và 2 học sinh nữ”
Số cách chọn 1 học sinh nam và 2 học sinh nữ: \(C_{10}^1.C_6^2 = 150\) (cách chọn)
Do đó, \(P\left( {X = 1} \right)\; = \frac{{150}}{{560}} = \frac{{15}}{{56}}\)
+ Biến cố \(\left\{ {X = 2} \right\}\) là: “Chọn được 2 học sinh nam và 1 học sinh nữ”
Số cách chọn 2 học sinh nam và 1 học sinh nữ: \(C_{10}^2.C_6^1 = 270\) (cách chọn)
Do đó, \(P\left( {X = 2} \right)\; = \frac{{270}}{{560}} = \frac{{27}}{{56}}\)
+ Biến cố \(\left\{ {X = 3} \right\}\) là : “Chọn được 3 học sinh nam”
Số cách chọn 3 học sinh nam: \(C_{10}^3 = 120\) (cách chọn)
Do đó, \(P\left( {X = 3} \right)\; = \frac{{120}}{{560}} = \frac{{12}}{{56}}\)
Ta có bảng phân phối xác suất của X là:
Trả lời câu hỏi Vận dụng 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một trò chơi sử dụng một hộp đựng 20 quả cầu có kích thước và khối lượng như nhau được ghi số từ 1 đến 20. Người chơi lấy ngẫu nhiên đồng thời 3 quả cầu trong hộp. Gọi X là số lớn nhất ghi trên 3 quả cầu đã lấy ra.
a) Lập bảng phân bố xác suất của X.
b) Người chơi thắng cuộc nếu trong 3 quả cầu lấy ra có ít nhất 1 quả cầu ghi số lớn hơn 18. Tính xác suất thắng của người chơi.
Phương pháp giải:
Làm theo hướng dẫn trong sách
Lời giải chi tiết:
a) Tập các giá trị có thể của X là {3; 4;...; 20}
Số kết quả có thể là \(C_{20}^3 = 1140.\)
Biến cố \(\left\{ {X = k} \right\}\) là biến cố: “Trong 3 quả cầu lấy ra có 1 quả cầu đánh số \(k\) và 2 quả cầu đánh số nhỏ hơn \(k\)”. Số kết quả thuận lợi là: \(C_{k - 1}^2\)
Vậy \(P\left( {X = k} \right) = \frac{{C_{k - 1}^2}}{{C_{20}^3}} = \frac{{(k - 1)(k - 2)}}{{2280}}\)
Bảng phân bố xác suất của X là:

b) Biến cố: “Người chơi thắng” là biến cố hợp của hai biến cố \(A = \left\{ {X = 19} \right\}\) và \(B = \left\{ {X = 20} \right\}\)
Vì \(A,B\) là hai biến cố xung khắc nên
\(P(A \cup B) = P(A) + P(B){\rm{ = }}P(X = 19) + P(X = 20) = 0,134 + 0,15 = 0,284\)
Trả lời câu hỏi Hoạt động 2 trang 7 Chuyên đề học tập Toán 12 Kết nối tri thức
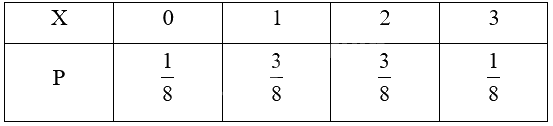
Hãy nêu số thích hợp với dấu “?” để hoàn thành bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) trong Ví dụ 1.

Phương pháp giải:
Dựa vào HĐ1, ta điền các kết quả tương ứng vào bảng
Lời giải chi tiết:
Trả lời câu hỏi Hoạt động 1 trang 6 Chuyên đề học tập Toán 12 Kết nối tri thức
Gieo một con xúc xắc cân đối, đồng chất liên tiếp 6 lần. Gọi \(X\)là số lần xúc xắc xuất hiện mặt 6 chấm trong 6 lần gieo liên tiếp đó
a) Các giá trị có thể của \(X\) là gì?
b) Trước khi thực hiện việc gieo xúc xắc đó, ta có khẳng định trước được \(X\) sẽ nhận giá trị nào không?
Phương pháp giải:
Dựa vào thực nghiệm gieo một con xúc xắc 6 lần
Lời giải chi tiết:
a) \(X \in \left\{ {0;1;2;3;4;5;6} \right\}\).
b) Ta không thể khẳng định trước được.
Trả lời câu hỏi Hoạt động 2 trang 7 Chuyên đề học tập Toán 12 Kết nối tri thức
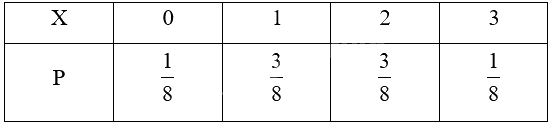
Hãy nêu số thích hợp với dấu “?” để hoàn thành bảng phân bố xác suất của biến ngẫu nhiên rời rạc \(X\) trong Ví dụ 1.

Phương pháp giải:
Dựa vào HĐ1, ta điền các kết quả tương ứng vào bảng
Lời giải chi tiết:
Trả lời câu hỏi Luyện tập 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một tổ có 10 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên đồng thời 3 học sinh. Gọi X là số học sinh nam trong 3 học sinh được chọn. Lập bảng phân bố xác suất của X.
Phương pháp giải:
Bước 1: Liệt kê các giá trị có thể của X
Bước 2: Tính các xác suất để X nhận các giá trị đó
Bước 3: Lập bảng phân bố xác suất cho biến ngẫu nhiên X
Lời giải chi tiết:
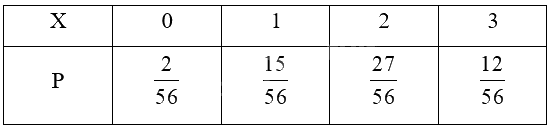
Các giá trị của X có thể nhận được thuộc tập {0; 1; 2; 3}.
Số kết quả có thể là \(C_{16}^3 = 560.\)
+ Biến cố \(\left\{ {X = 0} \right\}\) là: “Không có HS nam nào trong 3 HS được chọn”
Số cách chọn 3 học sinh nữ: \(C_6^3 = 20\) (cách chọn)
Do đó, \(P\left( {X = 0} \right)\; = \frac{{20}}{{560}} = \frac{2}{{56}}\)
+ Biến cố \(\left\{ {X = 1} \right\}\) là: “Chọn được 1 học sinh nam và 2 học sinh nữ”
Số cách chọn 1 học sinh nam và 2 học sinh nữ: \(C_{10}^1.C_6^2 = 150\) (cách chọn)
Do đó, \(P\left( {X = 1} \right)\; = \frac{{150}}{{560}} = \frac{{15}}{{56}}\)
+ Biến cố \(\left\{ {X = 2} \right\}\) là: “Chọn được 2 học sinh nam và 1 học sinh nữ”
Số cách chọn 2 học sinh nam và 1 học sinh nữ: \(C_{10}^2.C_6^1 = 270\) (cách chọn)
Do đó, \(P\left( {X = 2} \right)\; = \frac{{270}}{{560}} = \frac{{27}}{{56}}\)
+ Biến cố \(\left\{ {X = 3} \right\}\) là : “Chọn được 3 học sinh nam”
Số cách chọn 3 học sinh nam: \(C_{10}^3 = 120\) (cách chọn)
Do đó, \(P\left( {X = 3} \right)\; = \frac{{120}}{{560}} = \frac{{12}}{{56}}\)
Ta có bảng phân phối xác suất của X là:
Trả lời câu hỏi Vận dụng 1 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Một trò chơi sử dụng một hộp đựng 20 quả cầu có kích thước và khối lượng như nhau được ghi số từ 1 đến 20. Người chơi lấy ngẫu nhiên đồng thời 3 quả cầu trong hộp. Gọi X là số lớn nhất ghi trên 3 quả cầu đã lấy ra.
a) Lập bảng phân bố xác suất của X.
b) Người chơi thắng cuộc nếu trong 3 quả cầu lấy ra có ít nhất 1 quả cầu ghi số lớn hơn 18. Tính xác suất thắng của người chơi.
Phương pháp giải:
Làm theo hướng dẫn trong sách
Lời giải chi tiết:
a) Tập các giá trị có thể của X là {3; 4;...; 20}
Số kết quả có thể là \(C_{20}^3 = 1140.\)
Biến cố \(\left\{ {X = k} \right\}\) là biến cố: “Trong 3 quả cầu lấy ra có 1 quả cầu đánh số \(k\) và 2 quả cầu đánh số nhỏ hơn \(k\)”. Số kết quả thuận lợi là: \(C_{k - 1}^2\)
Vậy \(P\left( {X = k} \right) = \frac{{C_{k - 1}^2}}{{C_{20}^3}} = \frac{{(k - 1)(k - 2)}}{{2280}}\)
Bảng phân bố xác suất của X là:

b) Biến cố: “Người chơi thắng” là biến cố hợp của hai biến cố \(A = \left\{ {X = 19} \right\}\) và \(B = \left\{ {X = 20} \right\}\)
Vì \(A,B\) là hai biến cố xung khắc nên
\(P(A \cup B) = P(A) + P(B){\rm{ = }}P(X = 19) + P(X = 20) = 0,134 + 0,15 = 0,284\)
Mục 1 của Chuyên đề học tập Toán 12 - Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về đạo hàm. Đây là một phần quan trọng trong chương trình Toán 12, đóng vai trò nền tảng cho việc giải quyết các bài toán phức tạp hơn trong các chuyên đề tiếp theo. Việc nắm vững các khái niệm và kỹ năng liên quan đến đạo hàm là điều kiện cần thiết để đạt kết quả tốt trong kỳ thi THPT Quốc gia.
Các bài tập trên trang 6 tập trung vào việc tính đạo hàm của các hàm số lượng giác cơ bản như sinx, cosx, tanx, cotx. Để giải quyết các bài tập này, học sinh cần nắm vững các công thức đạo hàm của các hàm số lượng giác và áp dụng linh hoạt các quy tắc tính đạo hàm như quy tắc chuỗi, quy tắc tích, quy tắc thương.
Trang 7 giới thiệu các bài tập về đạo hàm của hàm số mũ và hàm số logarit. Học sinh cần nắm vững các công thức đạo hàm của các hàm số này và áp dụng các quy tắc tính đạo hàm tương tự như trên.
Các bài tập trên trang 8 yêu cầu học sinh tính đạo hàm của các hàm hợp. Đây là một dạng bài tập đòi hỏi học sinh phải áp dụng quy tắc chuỗi một cách chính xác. Quy tắc chuỗi phát biểu rằng đạo hàm của hàm hợp f(g(x)) bằng f'(g(x)) * g'(x).
Ví dụ: Để tính đạo hàm của hàm số y = sin(x^2), ta áp dụng quy tắc chuỗi như sau: y' = cos(x^2) * 2x.
Trang 9 cung cấp các bài tập tổng hợp, kết hợp nhiều kiến thức và kỹ năng về đạo hàm đã học. Các bài tập này giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán một cách toàn diện.
Để giải bài tập đạo hàm hiệu quả, học sinh cần:
Đạo hàm có nhiều ứng dụng quan trọng trong thực tế, bao gồm:
Hy vọng với bộ giải chi tiết này, các em học sinh sẽ tự tin hơn trong việc học tập và giải quyết các bài tập về đạo hàm. Chúc các em học tốt và đạt kết quả cao trong kỳ thi THPT Quốc gia!