Bài 2.12 trang 44 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, cùng với các phương pháp giải khác nhau để bạn có thể nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết và các kiến thức liên quan ngay sau đây!
Một nhà máy sản xuất hai loại sản phẩm, mỗi sản phẩm yêu cầu sử dụng ba máy. Máy đầu tiên có thể được sử dụng nhiều nhất là 70 giờ, máy thứ hai nhiều nhất là 40 giờ và máy thứ ba nhiều nhất là 90 giờ. Sản phẩm thứ nhất cần 2 giờ trên máy 1, 1 giờ trên máy II và 1 giờ trên máy III; sản phẩm thứ hai cần 1 giờ cho mỗi máy I, II và 3 giờ trên máy III. Nếu lợi nhuận là 400 nghìn đồng/đơn vị cho sản phẩm thứ nhất và 600 nghìn đồng/đơn vị cho sản phẩm thứ hai, thì cần sản xuất bao nhiều đơn vị mỗi sản
Đề bài
Một nhà máy sản xuất hai loại sản phẩm, mỗi sản phẩm yêu cầu sử dụng ba máy. Máy đầu tiên có thể được sử dụng nhiều nhất là 70 giờ, máy thứ hai nhiều nhất là 40 giờ và máy thứ ba nhiều nhất là 90 giờ. Sản phẩm thứ nhất cần 2 giờ trên máy 1, 1 giờ trên máy II và 1 giờ trên máy III; sản phẩm thứ hai cần 1 giờ cho mỗi máy I, II và 3 giờ trên máy III. Nếu lợi nhuận là 400 nghìn đồng/đơn vị cho sản phẩm thứ nhất và 600 nghìn đồng/đơn vị cho sản phẩm thứ hai, thì cần sản xuất bao nhiều đơn vị mỗi sản phẩm để lợi nhuận thu được là lớn nhất?
Phương pháp giải - Xem chi tiết
F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của ngũ giác. Tính giá trị của F(x; y) tại các điểm cực biên.
Lời giải chi tiết
Gọi x và y lần lượt là số sản phẩm thứ nhất và sản phẩm thứ hai cần sản xuất.
Lợi nhuận thu được là: 400x + 600y (nghìn đồng).
Ta có hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\2x + y \le 70\\x + y \le 40\\x + 3y \le 90\end{array} \right.\)
Miền nghiệm của hệ bất phương trình này là miền ngũ giác OABCD được tô màu như hình vẽ dưới đây:
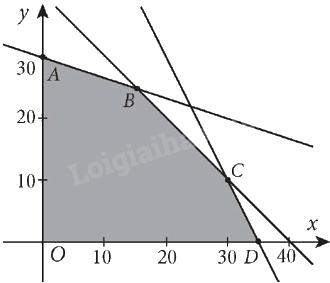
Các điểm cực biên là: O(0; 0), A(0; 30), B(15; 25), C(30; 10), D(35; 0).
Ta có: \(F(0;0) = 0,F(0,30) = 18000;F(15;25) = 21000;F(30;10) = 18000;F(35;0) = 14000\)
Vậy lợi nhuận thu được lớn nhất là 21 000 nghìn đồng khi x = 15 và y = 25, tức là cần sản xuất 15 sản phẩm thứ nhất và 25 sản phẩm thứ hai.
Bài 2.12 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để tìm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
(Giả sử bài toán cụ thể là: Tìm cực trị của hàm số f(x) = x^3 - 3x^2 + 2)
Bước 1: Tập xác định
Hàm số f(x) = x^3 - 3x^2 + 2 xác định trên tập số thực R.
Bước 2: Tính đạo hàm bậc nhất
f'(x) = 3x^2 - 6x
Bước 3: Tìm điểm dừng
Giải phương trình f'(x) = 0:
3x^2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2 là các điểm dừng.
Bước 4: Khảo sát dấu của đạo hàm
Lập bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Bước 5: Kết luận về cực trị
Dựa vào bảng xét dấu, ta có:
Ngoài bài 2.12, chuyên đề học tập Toán 12 - Kết nối tri thức còn nhiều bài tập tương tự về cực trị hàm số. Để giải các bài tập này, bạn cần nắm vững các kiến thức sau:
Các bài tập khác có thể yêu cầu tìm cực trị của hàm số trên một khoảng, hoặc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn. Phương pháp giải tương tự như bài 2.12, nhưng cần chú ý đến điều kiện của bài toán.
Để học tốt chuyên đề về đạo hàm và ứng dụng của đạo hàm, bạn nên:
Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!