Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 Chuyên đề học tập - Kết nối tri thức. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2, trang 26, 27, 28 và 29.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, giaitoan.edu.vn luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Ta giải bài toán Tình huống mở đầu. Từ HĐ1 ta có bài toán quy hoạch tuyến tính sau: F(x; y) = 40x + 30y → max Với các ràng buộc (left{ begin{array}{l}x + 2y le 100\2x + y le 80\x ge 0,y ge 0end{array} right.) Miền chấp nhận được S của bài toán là miền tứ giác tô màu trong Hình 2.3. a) Tìm tập hợp các điểm M(x; y) thỏa mãn F(x; y) = 40x + 30y = 1 200. b) Với mỗi số thực m xét đường thẳng dm¬: 40x + 30y = m. Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅. c) Từ câu b suy ra gi
Trả lời câu hỏi Luyện tập 2 trang 26 Chuyên đề học tập Toán 12 Kết nối tri thức
Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Phải thuê bao nhiêu xe loại A và bao nhiêu xe loại B để chi phí bỏ ra là ít nhất mà vẫn chở được hết hàng và người?
Phương pháp giải:
Vẽ miền nghiệm. Tìm giao điểm các đường thẳng bờ của miền nghiệm, thay tọa độ vào hàm số xem giá trị nào lớn nhất.
Lời giải chi tiết:
Gọi x và y lần lượt là số xe loại A và loại B cần thuê.
Chi phí thuê xe là: F(x; y) = 4x + 3y (triệu đồng).
Hệ bất phương trình ràng buộc x và y là:
\(\left\{ \begin{array}{l}20x + 10y \ge 140\\0,6x + 1,5y \ge 9\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\)
Miền nghiệm của hệ bất phương trình trên là miền tứ giác ABCD trong hình vẽ dưới đây:
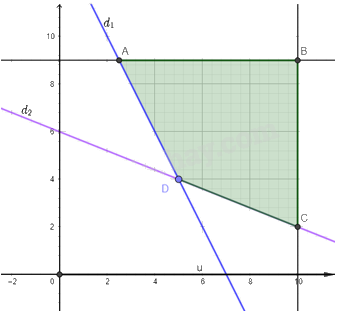
Các điểm cực biên là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).
Ta có:
F(2,5; 9) = 4.2,5 + 3.9 = 37;
F(10; 9) = 4.10 + 3.9 = 67;
F(10; 2) = 4.10 + 3.2 = 46;
F(5; 4) = 4.5 + 3.4 = 32.
Giá trị nhỏ nhất của F(x; y) bằng 32 tại D(5; 4)
Vậy chi phí thuê xe thấp nhất là 32 triệu đồng khi thuê 5 xe loại A và 4 xe loại B.
Trả lời câu hỏi Hoạt động 2 trang 16 Chuyên đề học tập Toán 12 Kết nối tri thức
Ta giải bài toán Tình huống mở đầu.
Từ HĐ1 ta có bài toán quy hoạch tuyến tính sau:
F(x; y) = 40x + 30y → max
Với các ràng buộc
\(\left\{ \begin{array}{l}x + 2y \le 100\\2x + y \le 80\\x \ge 0,y \ge 0\end{array} \right.\)
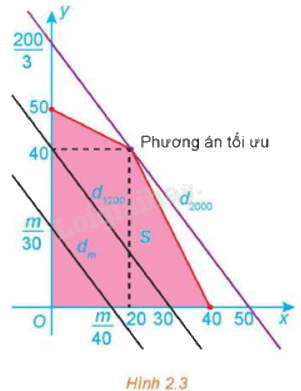
Miền chấp nhận được S của bài toán là miền tứ giác tô màu trong Hình 2.3.
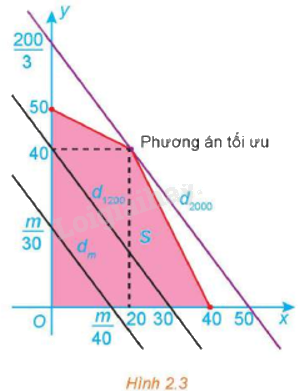
a) Tìm tập hợp các điểm M(x; y) thỏa mãn F(x; y) = 40x + 30y = 1 200.
b) Với mỗi số thực m xét đường thẳng dm: 40x + 30y = m.
Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅.
c) Từ câu b suy ra giá trị lớn nhất của F(x; y) trên miền S, từ đó suy ra lời giải của bài toán.
Phương pháp giải:
Vẽ miền nghiệm. Tìm giao điểm các đường thẳng bờ của miền nghiệm, thay tọa độ vào hàm số xem giá trị nào lớn nhất.
Lời giải chi tiết:
a) Tập hợp điểm M(x; y) là tập các điểm nằm trên đường thẳng d: 4x + 3y = 120 nằm trong miền chấp nhận S, chính là tập hợp các điểm nằm trên đoạn thẳng đi qua điểm (30;0) và (0;40).
b) Từ hình vẽ, ta thấy đường thẳng dm: 40x + 30y = m luôn cắt trục tung tại điểm có tung độ \(y = \frac{m}{{30}}\).
Để dm ∩ S ≠ ∅ thì \(0 \le \frac{m}{{30}} \le \frac{{200}}{3}\) hay \(0 \le m \le 2{\rm{ }}000\).
Vậy 0 ≤ m ≤ 2 000.
c) Ta có: F(x; y) = 40x + 30y = m, mà theo kết quả của câu b, ta có 0 ≤ m ≤ 2 000 nên 0 ≤ F(x; y) ≤ 2 000.
Vậy giá trị lớn nhất của F(x; y) trên miền S là 2 000.
Lời giải của bài toán:
Gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.
Lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II là: F(x; y) = 40x + 30y (nghìn đồng).
Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).
Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).
Vì xí nghiệp có 200 kg nguyên liệu (lượng nguyên liệu sử dụng không vượt quá lượng có sẵn) và tối đa 1 200 giờ làm việc nên ta có hệ:
\(\left\{ \begin{array}{l}2x + 4y \le 200\\30x + 15y \le 1{\rm{ }}200\\x \ge 0,y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y \le 100\\2x + y \le 80\\x \ge 0,y \ge 0\end{array} \right.\)
Miền nghiệm của hệ bất phương trình trên là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d1: x + 2y = 100 và đường thẳng d2: 2x + y = 80.
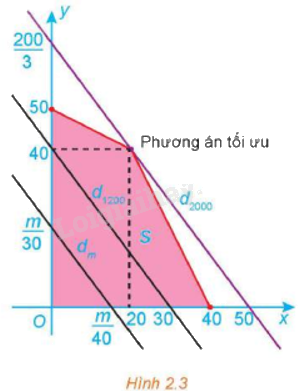
Ta có: F(20;40) = 2 000; F(0;50) = 1 500; F(0;40) = 1 200; F(0;0) = 0.
Giá trị lớn nhất của F(x; y) trên miền S là 2 000.
Vậy lợi nhuận cao nhất mà xí nghiệp đạt được là 2 000 nghìn đồng, tức 2 triệu đồng khi sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II.
Trả lời câu hỏi Hoạt động 2 trang 16 Chuyên đề học tập Toán 12 Kết nối tri thức
Ta giải bài toán Tình huống mở đầu.
Từ HĐ1 ta có bài toán quy hoạch tuyến tính sau:
F(x; y) = 40x + 30y → max
Với các ràng buộc
\(\left\{ \begin{array}{l}x + 2y \le 100\\2x + y \le 80\\x \ge 0,y \ge 0\end{array} \right.\)
Miền chấp nhận được S của bài toán là miền tứ giác tô màu trong Hình 2.3.
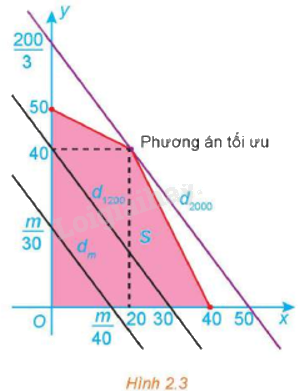
a) Tìm tập hợp các điểm M(x; y) thỏa mãn F(x; y) = 40x + 30y = 1 200.
b) Với mỗi số thực m xét đường thẳng dm: 40x + 30y = m.
Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅.
c) Từ câu b suy ra giá trị lớn nhất của F(x; y) trên miền S, từ đó suy ra lời giải của bài toán.
Phương pháp giải:
Vẽ miền nghiệm. Tìm giao điểm các đường thẳng bờ của miền nghiệm, thay tọa độ vào hàm số xem giá trị nào lớn nhất.
Lời giải chi tiết:
a) Tập hợp điểm M(x; y) là tập các điểm nằm trên đường thẳng d: 4x + 3y = 120 nằm trong miền chấp nhận S, chính là tập hợp các điểm nằm trên đoạn thẳng đi qua điểm (30;0) và (0;40).
b) Từ hình vẽ, ta thấy đường thẳng dm: 40x + 30y = m luôn cắt trục tung tại điểm có tung độ \(y = \frac{m}{{30}}\).
Để dm ∩ S ≠ ∅ thì \(0 \le \frac{m}{{30}} \le \frac{{200}}{3}\) hay \(0 \le m \le 2{\rm{ }}000\).
Vậy 0 ≤ m ≤ 2 000.
c) Ta có: F(x; y) = 40x + 30y = m, mà theo kết quả của câu b, ta có 0 ≤ m ≤ 2 000 nên 0 ≤ F(x; y) ≤ 2 000.
Vậy giá trị lớn nhất của F(x; y) trên miền S là 2 000.
Lời giải của bài toán:
Gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.
Lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II là: F(x; y) = 40x + 30y (nghìn đồng).
Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).
Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).
Vì xí nghiệp có 200 kg nguyên liệu (lượng nguyên liệu sử dụng không vượt quá lượng có sẵn) và tối đa 1 200 giờ làm việc nên ta có hệ:
\(\left\{ \begin{array}{l}2x + 4y \le 200\\30x + 15y \le 1{\rm{ }}200\\x \ge 0,y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y \le 100\\2x + y \le 80\\x \ge 0,y \ge 0\end{array} \right.\)
Miền nghiệm của hệ bất phương trình trên là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d1: x + 2y = 100 và đường thẳng d2: 2x + y = 80.
Ta có: F(20;40) = 2 000; F(0;50) = 1 500; F(0;40) = 1 200; F(0;0) = 0.
Giá trị lớn nhất của F(x; y) trên miền S là 2 000.
Vậy lợi nhuận cao nhất mà xí nghiệp đạt được là 2 000 nghìn đồng, tức 2 triệu đồng khi sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II.
Trả lời câu hỏi Luyện tập 2 trang 26 Chuyên đề học tập Toán 12 Kết nối tri thức
Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Phải thuê bao nhiêu xe loại A và bao nhiêu xe loại B để chi phí bỏ ra là ít nhất mà vẫn chở được hết hàng và người?
Phương pháp giải:
Vẽ miền nghiệm. Tìm giao điểm các đường thẳng bờ của miền nghiệm, thay tọa độ vào hàm số xem giá trị nào lớn nhất.
Lời giải chi tiết:
Gọi x và y lần lượt là số xe loại A và loại B cần thuê.
Chi phí thuê xe là: F(x; y) = 4x + 3y (triệu đồng).
Hệ bất phương trình ràng buộc x và y là:
\(\left\{ \begin{array}{l}20x + 10y \ge 140\\0,6x + 1,5y \ge 9\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\)
Miền nghiệm của hệ bất phương trình trên là miền tứ giác ABCD trong hình vẽ dưới đây:
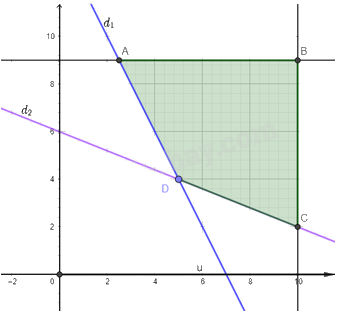
Các điểm cực biên là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).
Ta có:
F(2,5; 9) = 4.2,5 + 3.9 = 37;
F(10; 9) = 4.10 + 3.9 = 67;
F(10; 2) = 4.10 + 3.2 = 46;
F(5; 4) = 4.5 + 3.4 = 32.
Giá trị nhỏ nhất của F(x; y) bằng 32 tại D(5; 4)
Vậy chi phí thuê xe thấp nhất là 32 triệu đồng khi thuê 5 xe loại A và 4 xe loại B.
Mục 2 của Chuyên đề học tập Toán 12 - Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về các khái niệm và kỹ năng đã học trong chương trình. Các bài tập trong mục này thường yêu cầu học sinh vận dụng linh hoạt các công thức, định lý và phương pháp giải toán đã được trình bày trước đó. Việc giải quyết thành công các bài tập này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện tư duy logic và khả năng giải quyết vấn đề.
Các bài tập trên trang 26 thường tập trung vào việc kiểm tra kiến thức cơ bản về giới hạn của hàm số. Học sinh cần nắm vững định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn. Các bài tập có thể yêu cầu tính giới hạn của hàm số tại một điểm, xét tính liên tục của hàm số hoặc tìm các giá trị của tham số để hàm số có giới hạn tại một điểm.
Trang 27 tiếp tục đi sâu vào các bài tập về giới hạn, nhưng với mức độ khó hơn. Các bài tập có thể yêu cầu sử dụng các định lý giới hạn đặc biệt, như định lý giới hạn của dãy số hoặc định lý giới hạn của hàm số hợp. Ngoài ra, các bài tập cũng có thể yêu cầu học sinh chứng minh các tính chất của giới hạn hoặc giải các bài toán ứng dụng liên quan đến giới hạn.
Các bài tập trên trang 28 chuyển sang tập trung vào việc ôn tập và mở rộng kiến thức về đạo hàm. Học sinh cần nắm vững định nghĩa đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm trong việc giải các bài toán về cực trị, điểm uốn và khảo sát hàm số. Các bài tập có thể yêu cầu tính đạo hàm của hàm số, tìm các điểm cực trị của hàm số hoặc khảo sát sự biến thiên của hàm số.
Trang 29 tiếp tục đi sâu vào các bài tập về đạo hàm, nhưng với mức độ khó hơn. Các bài tập có thể yêu cầu sử dụng các phương pháp tính đạo hàm nâng cao, như đạo hàm hàm hợp hoặc đạo hàm hàm ẩn. Ngoài ra, các bài tập cũng có thể yêu cầu học sinh giải các bài toán ứng dụng liên quan đến đạo hàm, như bài toán tối ưu hóa hoặc bài toán liên quan đến tốc độ thay đổi.
Hy vọng rằng bài viết này đã cung cấp cho các em những thông tin hữu ích và giúp các em giải quyết thành công các bài tập trong mục 2 trang 26, 27, 28, 29 Chuyên đề học tập Toán 12 - Kết nối tri thức. Chúc các em học tập tốt!