Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 2.3 trang 33 thuộc Chuyên đề học tập Toán 12 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những phương pháp giải bài tập Toán 12 một cách logic và dễ tiếp thu, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Một nhà máy hóa chất sản xuất hai hợp chất X và Y. Khi sản xuất một đơn vị hợp chất X sẽ có 2 dm3 khí CO (carbon monoxide) và 6 dm3 khí SO2 (sulfur dioxide) phát tán ra môi trường. Khi sản xuất một đơn vị hợp chất Y sẽ có 4 dm3 khí CO và 3 dm3 khí SO2 phát tán ra môi trường. Các yêu cầu về khí thải chỉ cho phép nhà máy phát thải ra môi trường mỗi tuần không quá 3 000 dm3 khí CO và không quá 5 400 dm3 khí SO2. Nhà máy có thể bán hết tất cả các đơn vị hợp chất X và Y sản xuất ra với giá 36 000 đồn
Đề bài
Một nhà máy hóa chất sản xuất hai hợp chất X và Y. Khi sản xuất một đơn vị hợp chất X sẽ có 2 dm3 khí CO (carbon monoxide) và 6 dm3 khí SO2 (sulfur dioxide) phát tán ra môi trường. Khi sản xuất một đơn vị hợp chất Y sẽ có 4 dm3 khí CO và 3 dm3 khí SO2 phát tán ra môi trường. Các yêu cầu về khí thải chỉ cho phép nhà máy phát thải ra môi trường mỗi tuần không quá 3 000 dm3 khí CO và không quá 5 400 dm3 khí SO2. Nhà máy có thể bán hết tất cả các đơn vị hợp chất X và Y sản xuất ra với giá 36 000 đồng một đơn vị hợp chất X và 24 000 đồng một đơn vị hợp chất Y. Xác định số đơn vị hợp chất X và Y mỗi loại cần sản xuất trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường.
Phương pháp giải - Xem chi tiết
F(x; y) đạt giá trị lớn nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên
Lời giải chi tiết
Gọi x và y lần lượt là số đơn vị hợp chất X và Y cần sản xuất.
Lợi nhuận thu được là: F(x; y) = 36 000x + 24 000y (đồng).
Ta có hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\2{\rm{x}} + 4y \le 3{\rm{ }}000\\6{\rm{x}} + 3y \le {\rm{5 400}}\end{array} \right.\)
Miền nghiệm của hệ bất phương trình này là miền tứ giác OABC được tô màu như hình vẽ dưới đây:
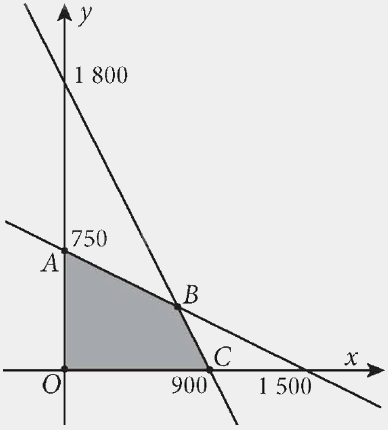
Các điểm cực biên là: O(0; 0), A(0; 750), B(700; 400), C(900; 0).
Ta có:
F(0; 0) = 36 000.0 + 24 000.0 = 0;
F(0; 750) = 36 000.0 + 24 000.750 = 18 000 000;
F(700; 400) = 36 000.700 + 24 000.400 = 34 800 000;
F(900; 0) = 36 000.900 + 24 000.0 = 32 400 000.
Giá trị lớn nhất của F(x; y) bằng 34 800 tại điểm cực biên B(700; 400).
Vậy cần sản xuất 700 đơn vị hợp chất X và 400 đơn vị hợp chất Y trong một tuần để thu được lợi nhuận cao nhất mà vẫn đảm bảo các yêu cầu về khí thải môi trường.
Bài 2.3 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 2.3 trang 33, học sinh cần xác định hàm số cần xét, khoảng xác định của hàm số và các yêu cầu cụ thể như tìm cực trị, khoảng đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Để giải bài 2.3 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức, học sinh có thể áp dụng các phương pháp sau:
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2. Ta sẽ tiến hành giải bài tập theo các bước sau:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Khi giải bài 2.3 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức, học sinh cần lưu ý những điều sau:
Bài tập 2.3 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức có ứng dụng thực tế trong nhiều lĩnh vực như kinh tế, kỹ thuật, vật lý. Ví dụ, trong kinh tế, đạo hàm được sử dụng để tính toán chi phí biên, doanh thu biên và lợi nhuận biên. Trong kỹ thuật, đạo hàm được sử dụng để tính toán vận tốc, gia tốc và các đại lượng liên quan đến chuyển động.
Hy vọng rằng hướng dẫn chi tiết này sẽ giúp bạn giải bài 2.3 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!