Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 2.1 trang 32 thuộc Chuyên đề học tập Toán 12 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những phương pháp giải bài tập Toán 12 một cách logic và dễ tiếp thu, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Một trung tâm tổ chức sự kiện có một phòng tổ chức lễ cưới với hai kiểu bàn ăn: bàn hình chữ nhật ngồi 6 người với giá thuê 200 nghìn đồng và bàn tròn ngồi 10 người với giá thuê 300 nghìn đồng. Anh Nam muốn thuê phòng để tổ chức đám cưới với 250 khách mời. Căn phòng chỉ chứa được tối đa 35 bàn các loại và chỉ có 15 bàn hình chữ nhật. Hỏi anh Nam phải thuê mỗi loại bàn bao nhiêu để giảm thiểu tối đa chi phí mà vẫn đáp ứng được các yêu cầu trên.
Đề bài
Một trung tâm tổ chức sự kiện có một phòng tổ chức lễ cưới với hai kiểu bàn ăn: bàn hình chữ nhật ngồi 6 người với giá thuê 200 nghìn đồng và bàn tròn ngồi 10 người với giá thuê 300 nghìn đồng. Anh Nam muốn thuê phòng để tổ chức đám cưới với 250 khách mời. Căn phòng chỉ chứa được tối đa 35 bàn các loại và chỉ có 15 bàn hình chữ nhật. Hỏi anh Nam phải thuê mỗi loại bàn bao nhiêu để giảm thiểu tối đa chi phí mà vẫn đáp ứng được các yêu cầu trên.
Phương pháp giải - Xem chi tiết
F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên
Lời giải chi tiết
Gọi x và y lần lượt là số bàn hình chữ nhật và số bàn tròn cần thuê.
Chi phí thuê bàn là: 200x + 300y (nghìn đồng).
Ta có hệ bất phương trình sau:
\(\left\{ \begin{array}{l}0 \le x \le 15,y \ge 0\\x + y \le 35\\6{\rm{x}} + 10y \ge 250\end{array} \right.\)
Miền nghiệm của hệ bất phương trình này là miền tứ giác ABCD được tô màu như hình vẽ dưới đây:
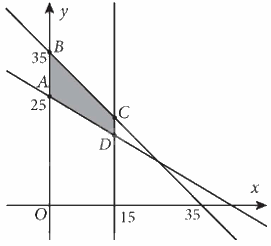
Các điểm cực biên là: A(0; 35), B(0; 25), C(15; 16), D(15; 20).
Ta có:
F(0; 35) = 200.0 + 300.35 = 10 500;
F(0; 25) = 200.0 + 300.25 = 7 500;
F(15; 16) = 200.15 + 300.16 = 7 800;
F(15; 20) = 200.15 + 300.20 = 9 000.
Giá trị nhỏ nhất của F(x; y) bằng 7 500 tại điểm cực biên B(0; 25)
Vậy anh Nam chỉ cần thuê 25 bàn tròn để giảm thiểu tối đa chi phí mà vẫn đáp ứng được các yêu cầu trên.
Bài 2.1 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, từ đó nâng cao khả năng tư duy và giải quyết vấn đề.
Bài tập 2.1 trang 32 thường bao gồm các dạng bài sau:
Để giải bài tập 2.1 trang 32 hiệu quả, bạn cần nắm vững các kiến thức sau:
Ví dụ: Tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại x = 1.
Giải:
f'(x) = 2x + 2
f'(1) = 2(1) + 2 = 4
Vậy, đạo hàm của hàm số f(x) tại x = 1 là 4.
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 2.1 trang 32 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!
| Công thức | Mô tả |
|---|---|
| f'(x) = limh→0 (f(x+h) - f(x))/h | Định nghĩa đạo hàm |
| (u + v)' = u' + v' | Đạo hàm của tổng |
| (u - v)' = u' - v' | Đạo hàm của hiệu |