Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 12. Bài viết này sẽ hướng dẫn bạn giải bài 2.4 trang 33 thuộc Chuyên đề học tập Toán 12 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những phương pháp giải bài tập Toán 12 một cách logic và dễ tiếp thu, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Chế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F1 và F2 mỗi đơn vị F1 giá 1 200 đồng và mỗi đơn vị F2 giá 720 đồng. Mỗi đơn vị thức ăn F1 chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F2 chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế độ hỗn hợp F1 và F2 sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng.
Đề bài
Chế độ ăn của một người yêu cầu mỗi ngày tối thiểu 400 đơn vị vitamin, 500 đơn vị khoáng chất và 1 400 đơn vị calo. Có hai loại thức ăn F1 và F2 mỗi đơn vị F1 giá 1 200 đồng và mỗi đơn vị F2 giá 720 đồng. Mỗi đơn vị thức ăn F1 chứa 2 đơn vị vitamin, 1 đơn vị khoáng chất và 4 đơn vị calo. Mỗi đơn vị thức ăn F2 chứa 1 đơn vị vitamin, 2 đơn vị khoáng chất và 4 đơn vị calo. Tìm chế độ hỗn hợp F1 và F2 sao cho chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng.
Phương pháp giải - Xem chi tiết
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết
Gọi x và y lần lượt là chế ăn hỗn hợp F1 và F2.
Chi phí cho thức ăn là: 1 200x + 720y (đồng).
Ta có hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x \ge 0;y \ge 0\\2{\rm{x}} + y \ge 400\\x + 2y \ge 500\\4{\rm{x}} + 4y \ge 1{\rm{ }}400\end{array} \right.\)
Miền nghiệm của hệ bất phương trình này là miền tô màu, không bị chặn như hình vẽ dưới đây:
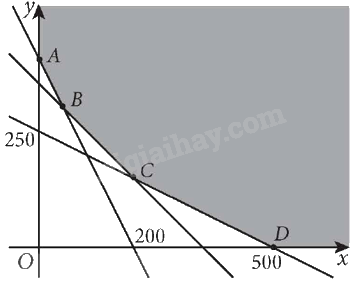
Các điểm cực biên là: A(0; 400), B(50; 300), C(200; 150), D(500; 0).
Ta có:
F(0; 400) = 1 200.0 + 720.400 = 288 000;
F(50; 300) = 1 200.50 + 720.300 = 276 000;
F(200; 150) = 1 200.200 + 720.150 = 348 000;
F(500; 0) = 1 200.500 + 720.0 = 600 000.
Do đó giá trị nhỏ nhất của F(x; y) bằng 276 000 tại điểm cực biên B(50; 300).
Vậy để chi phí là ít nhất mà vẫn đảm bảo các yêu cầu về dinh dưỡng thì cần 50 chế ăn loại F1 và 300 chế ăn loại F2.
Bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 2.4 trang 33, học sinh cần xác định hàm số cần xét, khoảng xác định của hàm số và các yêu cầu cụ thể như tìm cực trị, khoảng đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Để giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức, học sinh có thể áp dụng các phương pháp sau:
Giả sử hàm số cần xét là f(x) = x3 - 3x2 + 2. Ta sẽ tiến hành giải bài tập theo các bước sau:
Khi giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức, học sinh cần lưu ý những điều sau:
Việc giải bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức không chỉ giúp học sinh củng cố kiến thức về đạo hàm mà còn rèn luyện kỹ năng giải quyết vấn đề và tư duy logic. Những kiến thức này có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của cuộc sống, như kinh tế, kỹ thuật, khoa học tự nhiên.
Bài 2.4 trang 33 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong các kỳ thi.