Bài 2.7 trang 42 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết bài 2.7 trang 42 ngay dưới đây!
Người ta muốn kéo một đường dây điện tử nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C
Đề bài
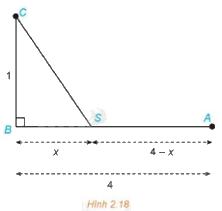
Người ta muốn kéo một đường dây điện tử nhà máy điện đặt tại điểm A đến một hòn đảo nhỏ C. Biết rằng nhà máy điện nằm sát bờ biển, bờ biển được coi là thẳng, khoảng cách CB từ hòn đảo C đến bờ biển là 1 km, khoảng cách giữa hai điểm A và B là 4 km. Mỗi kilômét dây nếu đặt ngầm dưới nước sẽ mất 5 000 USD, còn nếu đặt ngầm dưới đất sẽ mất 3 000 USD. Người ta dự định kéo dây điện ngầm dưới đất từ điểm A đến một điểm S trên bờ biển, nằm giữa A và B, sau đó chạy ngầm dưới nước từ điểm S đến hòn đảo C (Hình 2.18). Tìm vị trí điểm S sao cho chi phí kéo đường dây là nhỏ nhất.
Phương pháp giải - Xem chi tiết
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết
Đặt \(BS = x{\rm{ }}(m)\)\((0 \le x \le 4)\). Khi đó, \(SA = 4 - x;CS = \sqrt {1 + {x^2}} \)
Khi đó, chi phí cần bỏ ra là: \(f(x) = 5{\rm{ }}000\sqrt {1 + {x^2}} + 3{\rm{ }}000(4 - x)\), \(x \in \left[ {0;4} \right]\)
\(f'(x) = \frac{{5{\rm{ }}000x}}{{\sqrt {1 + {x^2}} }} - 3{\rm{ }}000\)
\(f'(x) = 0 \Leftrightarrow 3\sqrt {1 + {x^2}} = 5x \Leftrightarrow x = \frac{3}{4}\)
Ta có \(f(0) = 17{\rm{ }}000;f\left( {\frac{3}{4}} \right) = 16{\rm{ }}000;f(4) \approx 20{\rm{ }}616\). Ta thấy GTNN ứng với \(x = \frac{3}{4}\).
Vậy điểm S trên bờ biển cần tìm cách A một khoảng \(4 - \frac{3}{4} = \frac{{13}}{4}(km)\).
Bài 2.7 trang 42 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tối ưu hóa. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Bài 2.7 trang 42 thường có dạng bài toán tối ưu hóa hình học, ví dụ như tìm kích thước của một hình chữ nhật có diện tích cho trước mà chu vi nhỏ nhất, hoặc tìm kích thước của một hình hộp chữ nhật có thể tích cho trước mà diện tích bề mặt nhỏ nhất. Để giải quyết những bài toán này, chúng ta cần kết hợp kiến thức về đạo hàm với các công thức hình học.
Giả sử chúng ta cần tìm kích thước của một hình chữ nhật có diện tích là 100 cm2 sao cho chu vi nhỏ nhất. Gọi chiều dài và chiều rộng của hình chữ nhật lần lượt là x và y. Ta có:
Từ diện tích, ta có y = 100/x. Thay vào công thức chu vi, ta được P = 2(x + 100/x). Để tìm giá trị nhỏ nhất của P, ta tính đạo hàm của P theo x:
P' = 2(1 - 100/x2)
Giải phương trình P' = 0, ta được x = 10. Khi đó, y = 100/10 = 10. Vậy hình chữ nhật có chu vi nhỏ nhất là hình vuông có cạnh bằng 10 cm.
Khi giải các bài toán tối ưu hóa, cần chú ý đến tập xác định của hàm số và kiểm tra xem các điểm cực trị có thuộc tập xác định hay không. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính hợp lý của bài toán.
Kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán tối ưu hóa có ứng dụng rất lớn trong thực tế, ví dụ như trong kinh tế, kỹ thuật, và khoa học. Việc nắm vững kiến thức này giúp chúng ta giải quyết các vấn đề thực tế một cách hiệu quả và chính xác.
Bài 2.7 trang 42 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Bằng cách thực hiện các bước giải quyết bài toán một cách cẩn thận và chính xác, chúng ta có thể tìm ra lời giải đúng và hiểu sâu hơn về kiến thức toán học.
| Bước | Mô tả |
|---|---|
| 1 | Xác định hàm số |
| 2 | Tìm tập xác định |
| 3 | Tính đạo hàm |
| 4 | Tìm điểm cực trị |
| 5 | Xác định điểm cực đại, cực tiểu |
| 6 | Tính giá trị lớn nhất, nhỏ nhất |