Bài 2.13 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 12. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.13 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một công ty bản hàng toàn quốc đang lên kế hoạch tổ chức cuộc họp bán hàng tại Đà Nẵng. Giá vé máy bay khứ hồi thấp nhất từ Hà Nội đến Đà Nẵng là 2 triệu đồng và giá vé khứ hồi thấp nhất từ Thành phố Hồ Chí Minh đến Đà Nẵng là 2,4 triệu đồng. Có 28 đại diện bán hàng ở Hà Nội và 22 đại diện bán hàng ở Thành phố Hồ Chí Minh có thể đến Đà Nẵng dự cuộc họp này. Tổng cộng ít nhất 40 đại diện bản hàng từ Hà Nội và Thành phố Hồ Chí Minh phải tham dự cuộc họp này với ít nhất 12 người từ Hà Nội và 16 ngư
Đề bài
Một công ty bản hàng toàn quốc đang lên kế hoạch tổ chức cuộc họp bán hàng tại Đà Nẵng. Giá vé máy bay khứ hồi thấp nhất từ Hà Nội đến Đà Nẵng là 2 triệu đồng và giá vé khứ hồi thấp nhất từ Thành phố Hồ Chí Minh đến Đà Nẵng là 2,4 triệu đồng. Có 28 đại diện bán hàng ở Hà Nội và 22 đại diện bán hàng ở Thành phố Hồ Chí Minh có thể đến Đà Nẵng dự cuộc họp này. Tổng cộng ít nhất 40 đại diện bản hàng từ Hà Nội và Thành phố Hồ Chí Minh phải tham dự cuộc họp này với ít nhất 12 người từ Hà Nội và 16 người từ Thành phố Hồ Chí Minh. Cần cử bao nhiều đại diện bán hàng ở Hà Nội và bao nhiêu đại diện bán hàng ở Thành phố Hồ Chí Minh đến dự cuộc họp bán hàng ở Đà Nẵng để tổng chi phí về máy bay là nhỏ nhất?
Phương pháp giải - Xem chi tiết
F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các đỉnh của tứ giác
Lời giải chi tiết
Gọi x và y lần lượt là số đại diện bán hàng ở Hà Nội và Thành phố Hồ Chí Minh được cử đến dự cuộc họp bán hàng ở Đà Nẵng.
Tổng chi phí vé máy bay là: \(F(x,y) = 2x + 2,4y\) (triệu đồng).
Ta có hệ bất phương trình sau:
\(\left\{ \begin{array}{l}12 \le x \le 28\\16 \le y \le 22\\x + y \ge 40\end{array} \right.\)
Miền nghiệm của hệ bất phương trình này là miền tứ giác ABCD được tô màu dưới đây:
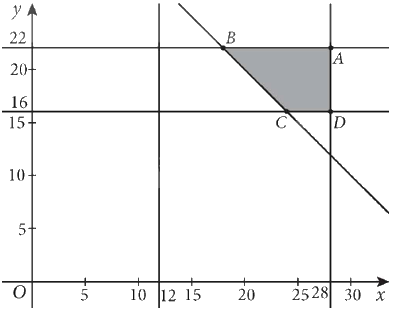
Các điểm cực biên là: A(18; 22), B(28; 22), C(28; 16), D(24; 16).
Ta có: \(F\left( {18;{\rm{ }}22} \right) = 88,8;F\left( {28;{\rm{ }}22} \right) = 108,8;F\left( {28;{\rm{ }}16} \right) = 94,4;F\left( {24;{\rm{ }}16} \right) = 86,4.\)
Vậy tổng chi phí vé máy bay nhỏ nhất là 86,4 triệu đồng khi x=24 và y=16 tức là cần cử 24 đại diện bán hàng ở Hà Nội và 16 đại diện bán hàng ở Thành phố Hồ Chí Minh đến dự cuộc họp.
Bài 2.13 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Nội dung bài tập:
Bài 2.13 yêu cầu học sinh tìm đạo hàm của hàm số và giải các bài toán liên quan đến ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Lời giải chi tiết:
Để giải bài 2.13, ta thực hiện các bước sau:
Ví dụ minh họa:
Giả sử hàm số f(x) = x3 - 3x2 + 2. Ta thực hiện các bước sau:
Bước 1: Tính đạo hàm: f'(x) = 3x2 - 6x
Bước 2: Tìm điểm cực trị: Giải phương trình 3x2 - 6x = 0, ta được x = 0 và x = 2.
Bước 3: Xác định loại cực trị: f''(x) = 6x - 6. Tại x = 0, f''(0) = -6 < 0, vậy x = 0 là điểm cực đại. Tại x = 2, f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.
Bước 4: Xác định khoảng đơn điệu:
Lưu ý:
Khi giải bài tập về đạo hàm, học sinh cần chú ý các quy tắc tính đạo hàm và các điều kiện để hàm số có cực trị. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính chính xác.
Tổng kết:
Bài 2.13 trang 44 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và dễ hiểu trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức Toán học. Chúc các em học tập tốt!