Bài 2.16 trang 45 Chuyên đề học tập Toán 12 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết và các phương pháp tiếp cận bài toán này ngay sau đây!
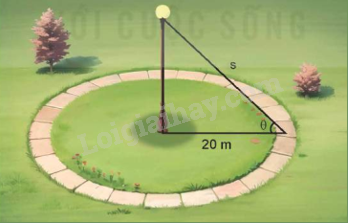
Một khu vực hình tròn có bán kính 20 m được bao quanh bởi một lối đi bộ (như hình vẽ). Một bóng đèn được lắp ở trên đỉnh cột nằm ở trung tâm của khu vực. Hỏi độ cao của cột đèn là bao nhiêu thì sẽ chiếu sáng mạnh nhất cho lối đi bộ? Biết rằng cường độ chiếu sáng cho bởi công thức \(I = \frac{{\sin \theta }}{s}\), trong đó s là khoảng cách từ nguồn sáng và \(\theta \) là góc mà ánh sáng chiếu vào bề mặt.
Đề bài
Một khu vực hình tròn có bán kính 20 m được bao quanh bởi một lối đi bộ (như hình vẽ). Một bóng đèn được lắp ở trên đỉnh cột nằm ở trung tâm của khu vực. Hỏi độ cao của cột đèn là bao nhiêu thì sẽ chiếu sáng mạnh nhất cho lối đi bộ? Biết rằng cường độ chiếu sáng cho bởi công thức \(I = \frac{{\sin \theta }}{s}\), trong đó s là khoảng cách từ nguồn sáng và \(\theta \) là góc mà ánh sáng chiếu vào bề mặt.
Phương pháp giải - Xem chi tiết
Sử dụng đạo hàm để giải quyết bài toán tối ưu.
Lời giải chi tiết
Gọi h là chiều cao của đèn (h>0,mét)
Ta có: \(I = \frac{{\sin \theta }}{s} = \frac{h}{{{s^2}}} = \frac{h}{{{h^2} + 400}}\)
Xét hàm số \(I(h) = \frac{h}{{{h^2} + 400}},h > 0\)
Ta có: \(I'(h) = \frac{{400 - {h^2}}}{{{{\left( {{h^2} + 400} \right)}^2}}}\)
\(I'(h) = 0 \Leftrightarrow h = 20\) (do \(h > 0\)).
Ta có bảng biến thiên:
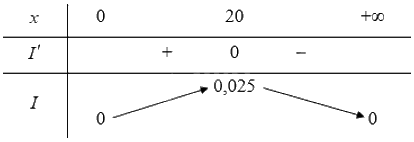
Vậy khi chiều cao của cột đèn là 20m thì sẽ chiếu sáng mạnh nhất cho lối đi bộ.
Bài 2.16 trang 45 Chuyên đề học tập Toán 12 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tối ưu hóa. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
(Nội dung lời giải chi tiết bài 2.16 trang 45 sẽ được trình bày tại đây. Bao gồm các bước giải cụ thể, các phép tính chính xác và giải thích rõ ràng từng bước. Ví dụ:)
Đề bài: (Ví dụ: Một người nông dân có 100m hàng rào để rào một mảnh đất hình chữ nhật. Tìm kích thước của mảnh đất để diện tích lớn nhất.)
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm và ứng dụng của đạo hàm, bạn có thể tham khảo các bài tập tương tự sau:
Khi giải các bài tập này, hãy nhớ áp dụng các bước giải đã trình bày ở trên và chú ý đến việc xác định đúng hàm số, tập xác định và các điểm cực trị. Ngoài ra, bạn có thể sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm giải toán để kiểm tra kết quả của mình.
Bài 2.16 trang 45 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Hy vọng rằng với lời giải chi tiết và các phương pháp giải đã trình bày, bạn sẽ tự tin hơn trong việc học tập và giải quyết các bài toán tương tự.