Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 24, 25, 26 của Chuyên đề học tập Toán 12 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong các kỳ thi.
Trong bài toán mở đầu, gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất. a) Kí hiệu F(x; y) là lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II. Viết biểu thức tính F(x; y) theo x và y. b) Lập hệ bất phương trình bậc nhất hai ẩn ràng buộc x và y thỏa mãn yêu cầu của bài toán. c) Biểu diễn trên mặt phẳng toạ độ để thấy rằng miền nghiệm của hệ bất phương trình tìm được trong ý b là một miền tứ giác. Tìm toạ độ các đỉnh của miền tứ giác
Trả lời câu hỏi Luyện tập 1 trang 26 Chuyên đề học tập Toán 12 Kết nối tri thức
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất X và 9 kg chất Y. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20 kg chất X và 0,6 kg chất Y. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất X và 1,5 kg chất Y. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đáp ứng được các yêu cầu đặt ra ở trên?
a) Đặt ẩn và viết bài toán quy hoạch tuyến tính diễn tả yêu cầu của bài toán trên.
b) Biểu diễn tập các phương án chấp nhận được và tìm các phương án cực biên.
Phương pháp giải:
Giải tương tự ví dụ 1,2
Lời giải chi tiết:
a) Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng (x ≥ 0, y ≥ 0).
Do cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên x ≤ 10, y ≤ 9.
Số kg chất X chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 20x + 10y (kg).
Số kg chất Y chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 0,6x + 1,5y (kg).
Theo bài, cần chiết xuất ít nhất 140 kg chất X và 9 kg chất Y nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}20x + 10y \ge 140\\0,6x + 1,5y \ge 9\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\)
Gọi F(x; y) là chi phí mua nguyen liệu, khi đó F(x; y) = 4x + 3y (triệu đồng).
Vậy ta có bài toán quy hoạch tuyến tính như sau:
F(x; y) = 4x + 3y → min
với các ràng buộc \(\left\{ \begin{array}{l}20x + 10y \ge 140\\0,6x + 1,5y \ge 9\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\)
b) Tập các phương án chấp nhận được là miền tứ giác ABCD được tô màu trong hình vẽ dưới đây:
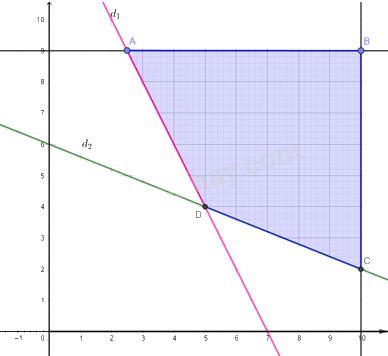
Các đỉnh của miền nghiệm là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).
Các đỉnh A,B,C, D là các phương án cực biên.
Trả lời câu hỏi Hoạt động 1 trang 24 Chuyên đề học tập Toán 12 Kết nối tri thức
Trong bài toán mở đầu, gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.
a) Kí hiệu F(x; y) là lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II. Viết biểu thức tính F(x; y) theo x và y.
b) Lập hệ bất phương trình bậc nhất hai ẩn ràng buộc x và y thỏa mãn yêu cầu của bài toán.
c) Biểu diễn trên mặt phẳng toạ độ để thấy rằng miền nghiệm của hệ bất phương trình tìm được trong ý b là một miền tứ giác. Tìm toạ độ các đỉnh của miền tứ giác này.
d) Tính giá trị của F(x; y) tại các đỉnh của miền tứ giác tìm được trong ý b, từ đó dự đoán về mức lợi nhuận cao nhất.
Phương pháp giải:
Dựa trên dữ kiện đề bài và các kiến thức đã học về bất phương trình bậc nhất hai ẩn, hệ bất phương trình bậc nhất hai ẩn
Lời giải chi tiết:
a) Lợi nhuận đem lại từ x kg sản phẩm loại I là 40x nghìn đồng.
Lợi nhuận đem lại từ y kg sản phẩm loại II là 30y nghìn đồng.
Khi đó, \(F\left( {x;y} \right) = 40x + 30y\) (nghìn đồng).
b) Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).
Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).
Vì xí nghiệp có 200 kg nguyên liệu và tối đa 1 200 giờ làm việc nên ta có:
\(\left\{ \begin{array}{l}2x + 4y \le 200\\30x + 15y \le 1{\rm{ }}200\\x \ge 0,y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y \le 100\\2x + y \le 80\\x \ge 0,y \ge 0\end{array} \right.\)
c) Miền nghiệm của hệ bất phương trình trong ý b là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d1: x + 2y = 100 và đường thẳng d2: 2x + y = 80.
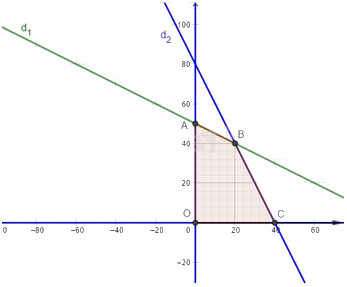
A là giao điểm của đường thẳng d1 với trục tung nên A(0; 50).
B là giao điểm của hai đường thẳng d1 và d2 nên B(20; 40).
C là giao điểm của đường thẳng d2 với trục hoành nên C(40; 0).
Vậy các đỉnh của miền nghiệm là: O(0; 0), A(0; 50), B(20; 40), C(40; 0).
d) Ta có:
\(\begin{array}{*{20}{l}}{F\left( {0;0} \right) = 40.0 + 30.0 = 0}\\{F\left( {0;50} \right) = 40.0 + 30.50 = 1{\rm{ }}500}\\{F\left( {20;40} \right) = 40.20 + 30.40 = 2{\rm{ }}000}\\{F\left( {40;0} \right) = {\rm{ }}40.40 + 30.0 = 1{\rm{ }}600}\end{array}\)
Dự đoán mức lợi nhuận cao nhất là 2 000 nghìn đồng, hay 2 triệu đồng.
Trả lời câu hỏi Hoạt động 1 trang 24 Chuyên đề học tập Toán 12 Kết nối tri thức
Trong bài toán mở đầu, gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.
a) Kí hiệu F(x; y) là lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II. Viết biểu thức tính F(x; y) theo x và y.
b) Lập hệ bất phương trình bậc nhất hai ẩn ràng buộc x và y thỏa mãn yêu cầu của bài toán.
c) Biểu diễn trên mặt phẳng toạ độ để thấy rằng miền nghiệm của hệ bất phương trình tìm được trong ý b là một miền tứ giác. Tìm toạ độ các đỉnh của miền tứ giác này.
d) Tính giá trị của F(x; y) tại các đỉnh của miền tứ giác tìm được trong ý b, từ đó dự đoán về mức lợi nhuận cao nhất.
Phương pháp giải:
Dựa trên dữ kiện đề bài và các kiến thức đã học về bất phương trình bậc nhất hai ẩn, hệ bất phương trình bậc nhất hai ẩn
Lời giải chi tiết:
a) Lợi nhuận đem lại từ x kg sản phẩm loại I là 40x nghìn đồng.
Lợi nhuận đem lại từ y kg sản phẩm loại II là 30y nghìn đồng.
Khi đó, \(F\left( {x;y} \right) = 40x + 30y\) (nghìn đồng).
b) Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).
Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).
Vì xí nghiệp có 200 kg nguyên liệu và tối đa 1 200 giờ làm việc nên ta có:
\(\left\{ \begin{array}{l}2x + 4y \le 200\\30x + 15y \le 1{\rm{ }}200\\x \ge 0,y \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + 2y \le 100\\2x + y \le 80\\x \ge 0,y \ge 0\end{array} \right.\)
c) Miền nghiệm của hệ bất phương trình trong ý b là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d1: x + 2y = 100 và đường thẳng d2: 2x + y = 80.
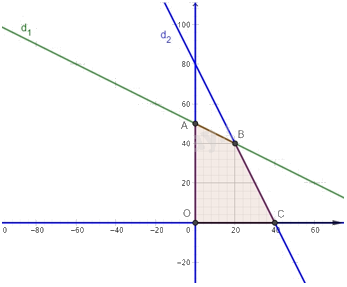
A là giao điểm của đường thẳng d1 với trục tung nên A(0; 50).
B là giao điểm của hai đường thẳng d1 và d2 nên B(20; 40).
C là giao điểm của đường thẳng d2 với trục hoành nên C(40; 0).
Vậy các đỉnh của miền nghiệm là: O(0; 0), A(0; 50), B(20; 40), C(40; 0).
d) Ta có:
\(\begin{array}{*{20}{l}}{F\left( {0;0} \right) = 40.0 + 30.0 = 0}\\{F\left( {0;50} \right) = 40.0 + 30.50 = 1{\rm{ }}500}\\{F\left( {20;40} \right) = 40.20 + 30.40 = 2{\rm{ }}000}\\{F\left( {40;0} \right) = {\rm{ }}40.40 + 30.0 = 1{\rm{ }}600}\end{array}\)
Dự đoán mức lợi nhuận cao nhất là 2 000 nghìn đồng, hay 2 triệu đồng.
Trả lời câu hỏi Luyện tập 1 trang 26 Chuyên đề học tập Toán 12 Kết nối tri thức
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất X và 9 kg chất Y. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng có thể chiết xuất được 20 kg chất X và 0,6 kg chất Y. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất X và 1,5 kg chất Y. Cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất mà vẫn đáp ứng được các yêu cầu đặt ra ở trên?
a) Đặt ẩn và viết bài toán quy hoạch tuyến tính diễn tả yêu cầu của bài toán trên.
b) Biểu diễn tập các phương án chấp nhận được và tìm các phương án cực biên.
Phương pháp giải:
Giải tương tự ví dụ 1,2
Lời giải chi tiết:
a) Gọi x, y lần lượt là số tấn nguyên liệu loại I và loại II cần dùng (x ≥ 0, y ≥ 0).
Do cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II nên x ≤ 10, y ≤ 9.
Số kg chất X chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 20x + 10y (kg).
Số kg chất Y chiết xuất được từ x tấn nguyên liệu loại I và y tấn nguyên liệu loại II là: 0,6x + 1,5y (kg).
Theo bài, cần chiết xuất ít nhất 140 kg chất X và 9 kg chất Y nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}20x + 10y \ge 140\\0,6x + 1,5y \ge 9\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\)
Gọi F(x; y) là chi phí mua nguyen liệu, khi đó F(x; y) = 4x + 3y (triệu đồng).
Vậy ta có bài toán quy hoạch tuyến tính như sau:
F(x; y) = 4x + 3y → min
với các ràng buộc \(\left\{ \begin{array}{l}20x + 10y \ge 140\\0,6x + 1,5y \ge 9\\0 \le x \le 10\\0 \le y \le 9\end{array} \right.\)
b) Tập các phương án chấp nhận được là miền tứ giác ABCD được tô màu trong hình vẽ dưới đây:
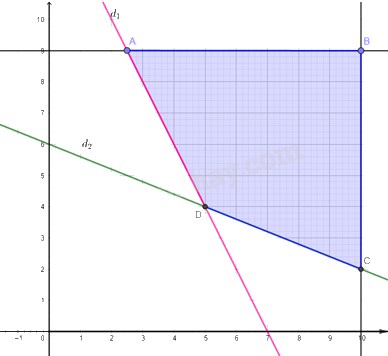
Các đỉnh của miền nghiệm là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).
Các đỉnh A,B,C, D là các phương án cực biên.
Mục 1 của Chuyên đề học tập Toán 12 - Kết nối tri thức thường tập trung vào một chủ đề quan trọng trong chương trình, ví dụ như đạo hàm, tích phân, hoặc các bài toán về hình học không gian. Việc nắm vững kiến thức nền tảng và phương pháp giải là yếu tố then chốt để giải quyết thành công các bài tập trong mục này.
Để hiểu rõ hơn về Mục 1, chúng ta cần xác định các nội dung chính mà nó bao gồm. Thông thường, mục này sẽ giới thiệu các khái niệm mới, định lý, tính chất quan trọng, và các ví dụ minh họa. Việc đọc kỹ sách giáo khoa và ghi chép đầy đủ là bước đầu tiên để nắm bắt kiến thức.
Có nhiều phương pháp giải bài tập khác nhau, tùy thuộc vào từng dạng bài cụ thể. Tuy nhiên, một số phương pháp chung có thể áp dụng cho hầu hết các bài tập trong Mục 1:
Chúng ta sẽ bắt đầu với việc giải chi tiết các bài tập trang 24. Mỗi bài tập sẽ được phân tích kỹ lưỡng, kèm theo lời giải chi tiết và các lưu ý quan trọng.
Tiếp theo, chúng ta sẽ giải chi tiết các bài tập trang 25. Các bài tập này có thể có độ khó cao hơn so với các bài tập trang 24, đòi hỏi người học phải có kiến thức vững chắc và kỹ năng giải toán tốt.
Cuối cùng, chúng ta sẽ giải chi tiết các bài tập trang 26. Các bài tập này thường là các bài tập tổng hợp, đòi hỏi người học phải vận dụng kiến thức từ nhiều phần khác nhau của Mục 1.
Trong quá trình giải bài tập, các em cần lưu ý một số điều sau:
Kiến thức trong Mục 1 có ứng dụng rất lớn trong thực tế và trong các kỳ thi. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán phức tạp một cách dễ dàng và hiệu quả.
Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ hiểu rõ hơn về Mục 1 trang 24, 25, 26 Chuyên đề học tập Toán 12 - Kết nối tri thức và đạt kết quả tốt nhất trong học tập.