Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 29, 30, 31, 32 Chuyên đề học tập Toán 12 - Kết nối tri thức. Bài viết này được giaitoan.edu.vn biên soạn nhằm hỗ trợ các em trong quá trình ôn tập và làm bài tập Toán 12.
Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, kèm theo các lưu ý quan trọng để giúp các em nắm vững kiến thức và đạt kết quả tốt nhất trong các kỳ thi.
Xét bài toán quy hoạch tuyến tính F(x; y) = 3x + 4y → min với các ràng buộc (left{ begin{array}{l}x ge 0,y ge 0\x + 2y ge 4\x + y ge 3end{array} right.) a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán. b) Tìm tập hợp các điểm M(x; y) thoả mãn F(x; y) = 3x + 4y = 12. c) Với mỗi số thực m, xét đường thẳng dm: 3x + 4y = m. Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅. d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận
Trả lời câu hỏi Luyện tập 3 trang 32 Chuyên đề học tập Toán 12 Kết nối tri thức
Giải bài toán quy hoạch tuyến tính sau:
F(x; y) = x + 2y → min
với các ràng buộc
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\x + y \ge 1\\2{\rm{x}} + 4y \ge 3\end{array} \right.\)
Phương pháp giải:
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết:
Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
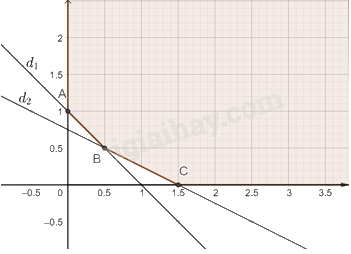
Có ba điểm cực biên là A(0; 1), B(0,5; 0,5), C(1,5; 0).
Ta có:
F(0; 1) = 2.
F(0,5; 0,5) = 1,5.
F(1,5; 0) = 1,5.
Vậy hệ có hai nghiệm thỏa mãn là B(0,5; 0,5) và C(1,5; 0).
Trả lời câu hỏi Hoạt động 3 trang 29 Chuyên đề học tập Toán 12 Kết nối tri thức
Xét bài toán quy hoạch tuyến tính
F(x; y) = 3x + 4y → min
với các ràng buộc
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\x + 2y \ge 4\\x + y \ge 3\end{array} \right.\)
a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.
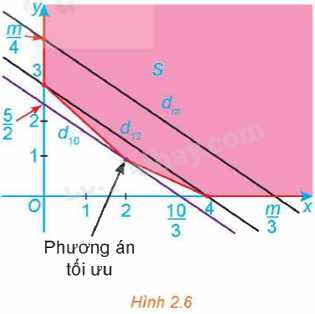
b) Tìm tập hợp các điểm M(x; y) thoả mãn
F(x; y) = 3x + 4y = 12.
c) Với mỗi số thực m, xét đường thẳng
dm: 3x + 4y = m.
Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅.
d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận được. Chứng tỏ rằng, giá trị nhỏ nhất này chính là giá trị của F(x; y) tại một điểm cực biên của miền chấp nhận được.
Phương pháp giải:
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết:
a) Ta thấy rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.
b) Theo bài, F(x; y) = 3x + 4y = 12.
Vậy tập hợp điểm M(x; y) thỏa mãn yêu cầu đề bài là tập hợp các điểm nằm trên đường thẳng d: 3x + 4y = 12 nằm trong miền S.
b) Vì đường thẳng dm song song với đường thẳng (d) nên đường thẳng dm: 3x + 4y = m luôn cắt trục tung tại điểm có tung độ \(y = \frac{m}{4}\).
Để dm ∩ S ≠ ∅ thì \(\frac{m}{4} \ge \frac{5}{2}\) hay m ≥ 10.
Vậy m ≥ 10.
c) Ta có: F(x; y) = 3x + 4y = m, mà theo kết quả của câu b, ta có m ≥ 10 nên F(x; y) ≥ 10.
Vậy giá trị nhỏ nhất của F(x; y) trên miền S là 10.
Ta có các điểm cực biên của miền S là: (0; 3), (2; 1), (4; 0).
⦁ F(0; 3) = 3.0 + 4.3 = 12;
⦁ F(2; 1) = 3.2 + 4.1 = 10;
⦁ F(4; 0) = 3.4 + 4.0 = 12.
Vậy giá trị nhỏ nhất của F(x; y) trên miền S chính là giá trị của F(x; y) tại điểm cực biên có tọa độ (2; 1) của miền chấp nhận được.
Trả lời câu hỏi Vận dụng trang 32 Chuyên đề học tập Toán 12 Kết nối tri thức
Một chủ trang trại cần sử dụng phân bón để chăm sóc cho một loại đậu tương. Loại đậu tương này cần ít nhất 18 đơn vị đạm và ít nhất 6 đơn vị phosphate. Ông chủ trang trại có thể sử dụng hai loại phân bón X và Y. Giá cả, hàm lượng đạm và hàm lượng phosphate có trong một tạ phân X và một tạ phân Y được cho bởi bảng sau:

Hãy cho biết cần phải mua bao nhiêu tạ phân loại X, bao nhiêu tạ phân loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên?
Phương pháp giải:
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết:
Gọi x, y lần lượt là số tạ phân bón loại X là Y cần phải mua.
Chi phí mua phân bón là: F(x; y) = 1,7x + 1,2y (triệu đồng).
Hệ bất phương trình ràng buộc x và y là
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\3x + 6y \ge 18\\2x + y \ge 6\end{array} \right.\)
Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
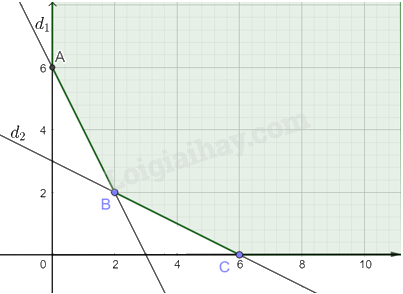
Các điểm cực biên là: A(0; 6), B(2; 2), C(6; 0).
Ta có:
F(0; 6) = 1,7.0 + 1,2.6 = 7,2
F(2; 2) = 1,7.2 + 1,2.2 = 5,8
F(6; 0) = 1,7.6 + 1,2.0 = 10,2
Do đó giá trị nhỏ nhất của F(x; y) bằng 5,8 triệu đồng tại điểm B(2; 2).
Vậy cần phải mua 2 tạ phân bón loại X và 2 tạ phân bón loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên.
Trả lời câu hỏi Hoạt động 3 trang 29 Chuyên đề học tập Toán 12 Kết nối tri thức
Xét bài toán quy hoạch tuyến tính
F(x; y) = 3x + 4y → min
với các ràng buộc
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\x + 2y \ge 4\\x + y \ge 3\end{array} \right.\)
a) Kiểm tra lại rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.
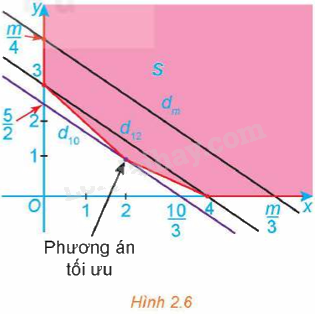
b) Tìm tập hợp các điểm M(x; y) thoả mãn
F(x; y) = 3x + 4y = 12.
c) Với mỗi số thực m, xét đường thẳng
dm: 3x + 4y = m.
Từ hình vẽ, tìm điều kiện của m để dm ∩ S ≠ ∅.
d) Từ phần c suy ra giá trị nhỏ nhất của F(x; y) trên miền chấp nhận được. Chứng tỏ rằng, giá trị nhỏ nhất này chính là giá trị của F(x; y) tại một điểm cực biên của miền chấp nhận được.
Phương pháp giải:
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết:
a) Ta thấy rằng miền S tô màu trong Hình 2.6 là miền chấp nhận được của bài toán.
b) Theo bài, F(x; y) = 3x + 4y = 12.
Vậy tập hợp điểm M(x; y) thỏa mãn yêu cầu đề bài là tập hợp các điểm nằm trên đường thẳng d: 3x + 4y = 12 nằm trong miền S.
b) Vì đường thẳng dm song song với đường thẳng (d) nên đường thẳng dm: 3x + 4y = m luôn cắt trục tung tại điểm có tung độ \(y = \frac{m}{4}\).
Để dm ∩ S ≠ ∅ thì \(\frac{m}{4} \ge \frac{5}{2}\) hay m ≥ 10.
Vậy m ≥ 10.
c) Ta có: F(x; y) = 3x + 4y = m, mà theo kết quả của câu b, ta có m ≥ 10 nên F(x; y) ≥ 10.
Vậy giá trị nhỏ nhất của F(x; y) trên miền S là 10.
Ta có các điểm cực biên của miền S là: (0; 3), (2; 1), (4; 0).
⦁ F(0; 3) = 3.0 + 4.3 = 12;
⦁ F(2; 1) = 3.2 + 4.1 = 10;
⦁ F(4; 0) = 3.4 + 4.0 = 12.
Vậy giá trị nhỏ nhất của F(x; y) trên miền S chính là giá trị của F(x; y) tại điểm cực biên có tọa độ (2; 1) của miền chấp nhận được.
Trả lời câu hỏi Luyện tập 3 trang 32 Chuyên đề học tập Toán 12 Kết nối tri thức
Giải bài toán quy hoạch tuyến tính sau:
F(x; y) = x + 2y → min
với các ràng buộc
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\x + y \ge 1\\2{\rm{x}} + 4y \ge 3\end{array} \right.\)
Phương pháp giải:
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết:
Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
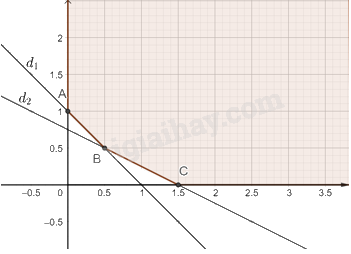
Có ba điểm cực biên là A(0; 1), B(0,5; 0,5), C(1,5; 0).
Ta có:
F(0; 1) = 2.
F(0,5; 0,5) = 1,5.
F(1,5; 0) = 1,5.
Vậy hệ có hai nghiệm thỏa mãn là B(0,5; 0,5) và C(1,5; 0).
Trả lời câu hỏi Vận dụng trang 32 Chuyên đề học tập Toán 12 Kết nối tri thức
Một chủ trang trại cần sử dụng phân bón để chăm sóc cho một loại đậu tương. Loại đậu tương này cần ít nhất 18 đơn vị đạm và ít nhất 6 đơn vị phosphate. Ông chủ trang trại có thể sử dụng hai loại phân bón X và Y. Giá cả, hàm lượng đạm và hàm lượng phosphate có trong một tạ phân X và một tạ phân Y được cho bởi bảng sau:

Hãy cho biết cần phải mua bao nhiêu tạ phân loại X, bao nhiêu tạ phân loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên?
Phương pháp giải:
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Vì miền chấp nhận được không là miền đa giác và có x ≥ 0, y ≥ 0 nên F(x; y) có giá trị nhỏ nhất trên S và đạt được tại một trong các điểm cực biên của miền chấp nhận được.
Lời giải chi tiết:
Gọi x, y lần lượt là số tạ phân bón loại X là Y cần phải mua.
Chi phí mua phân bón là: F(x; y) = 1,7x + 1,2y (triệu đồng).
Hệ bất phương trình ràng buộc x và y là
\(\left\{ \begin{array}{l}x \ge 0,y \ge 0\\3x + 6y \ge 18\\2x + y \ge 6\end{array} \right.\)
Miền nghiệm S của hệ bất phương trình không là miền đa giác và được tô màu như hình vẽ dưới đây:
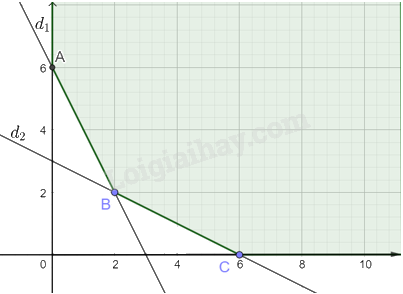
Các điểm cực biên là: A(0; 6), B(2; 2), C(6; 0).
Ta có:
F(0; 6) = 1,7.0 + 1,2.6 = 7,2
F(2; 2) = 1,7.2 + 1,2.2 = 5,8
F(6; 0) = 1,7.6 + 1,2.0 = 10,2
Do đó giá trị nhỏ nhất của F(x; y) bằng 5,8 triệu đồng tại điểm B(2; 2).
Vậy cần phải mua 2 tạ phân bón loại X và 2 tạ phân bón loại Y để chi phí là thấp nhất mà vẫn đảm bảo chế độ dinh dưỡng cho loại đậu tương trên.
Mục 3 trong Chuyên đề học tập Toán 12 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Việc giải các bài tập trang 29, 30, 31, 32 là cơ hội để học sinh củng cố kiến thức và rèn luyện kỹ năng giải quyết vấn đề.
Để hiểu rõ hơn về Mục 3, chúng ta cần xác định nội dung chính mà nó đề cập đến. Thông thường, Mục 3 sẽ đi sâu vào một trong các chủ đề sau:
Việc xác định đúng nội dung chính của Mục 3 là bước đầu tiên để giải quyết các bài tập một cách hiệu quả.
Để giải các bài tập trong Mục 3 trang 29, 30, 31, 32 Chuyên đề học tập Toán 12 - Kết nối tri thức, học sinh cần áp dụng các phương pháp giải phù hợp với từng dạng bài. Dưới đây là một số phương pháp thường được sử dụng:
Ngoài ra, học sinh cũng cần chú ý đến việc kiểm tra lại kết quả sau khi giải bài tập để đảm bảo tính chính xác.
Dưới đây là giải chi tiết các bài tập trang 29, 30, 31, 32 Chuyên đề học tập Toán 12 - Kết nối tri thức:
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
(Nội dung bài tập và lời giải chi tiết)
Lưu ý: Các lời giải chi tiết sẽ được trình bày một cách rõ ràng, dễ hiểu, kèm theo các bước giải cụ thể và các lưu ý quan trọng.
Sau khi đã giải các bài tập trong Mục 3, học sinh nên dành thời gian luyện tập thêm các bài tập tương tự để củng cố kiến thức và kỹ năng. Có rất nhiều nguồn tài liệu luyện tập khác nhau, bao gồm sách bài tập, đề thi thử, và các bài tập trực tuyến.
Việc luyện tập thường xuyên sẽ giúp học sinh tự tin hơn khi đối mặt với các bài toán khó và đạt kết quả tốt nhất trong các kỳ thi.
Giải mục 3 trang 29, 30, 31, 32 Chuyên đề học tập Toán 12 - Kết nối tri thức là một bước quan trọng trong quá trình học tập Toán 12. Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập một cách hiệu quả. Chúc các em học tập tốt!