Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 Chuyên đề học tập - Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong mục 2, trang 9, 10, 11, 12, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết mang đến cho các em những giải pháp học tập hiệu quả nhất.
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó?
Trả lời câu hỏi Hoạt động 3 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó?
Phương pháp giải:
Trung bình = Tổng số vụ tai nạn / số buổi tối thứ Bảy
Lời giải chi tiết:
Có: \(0.10 + 1.20 + 2.23 + 3.25 + 4.15 + 7.5 = 236\) vụ vi phạm trong 98 buổi tối thứ Bảy
Vậy trung bình có \(\frac{{236}}{{98}} \approx 2,408\) vụ vi phạm trọng 98 buổi tối thứ Bảy
Trả lời câu hỏi trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Trở lại HĐ4. Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2. Tính độ lệch chuẩn của X và Y.
Phương pháp giải:
Áp dụng công thức tính độ lệch chuẩn
Lời giải chi tiết:
\(\begin{array}{l}E(X) = 4\\V(X) = {\left( {8 - 4} \right)^2}.\frac{1}{3} + {\left( {2 - 4} \right)^2}.\frac{2}{3} = 8\\ \Rightarrow \sigma (X) = \sqrt 8 \approx 2,828.\end{array}\)
\(\begin{array}{l}E(Y) = 4\\V\left( Y \right) = {\left( {5 - 4} \right)^2}.\frac{1}{2} + {\left( {3 - 4} \right)^2}.\frac{1}{2} = 1\\ \Rightarrow \sigma \left( Y \right) = 1\end{array}\)
Trả lời câu hỏi Luyện tập 2 trang 10 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường vào tối thứ Bảy có thể là 0; 1; 2; 3; 4; 5 với các xác suất tương ứng là 0,1; 0,2; 0,25; 0,15 và 0,05. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường đó và tối thứ Bảy?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X
Bước 2: Tính kì vọng \(E(X)\) theo công thức
Lời giải chi tiết:
Gọi X là số vụ vi phạm Luật Giao thông đường bộ trên đoạn đường vào tối thứ Bảy. Khi đó, X là biến ngẫu nhiên rời rạc có bảng phân bố xác suất:

Ta có:
\(\;E(X) = 0,01 + 1.0,2 + 2.0,25 + 3.0,25 + 4.0,15 + 5.0,05 = 2,3\)
Vậy trên đoạn đường vào tối thứ Bảy có trung bình 2,3 vụ vi phạm Luật Giao thông đường bộ
Trả lời câu hỏi Vận dụng 2 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Tiếp tục xét tình huống mở đầu, giả sử ở vòng 1 Minh chọn câu hỏi loại II.
a) Hỏi trung bình Minh nhận được bao nhiêu điểm?
b) Ở vòng 1 Minh nên chọn loại câu hỏi nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên Y.
Bước 2: Tính kì vọng \(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Giả sử ở vòng 1 Minh chọn câu hỏi loại II. Gọi Y là số điểm Minh nhận được.
Gọi A là biến cố “Minh trả lời đúng câu hỏi loại I” \( \Rightarrow P\left( A \right) = 0,8\)
B là biến cố “Minh trả lời đúng câu hỏi loại II”. \( \Rightarrow P\left( B \right) = 0,6\)
+ Nếu trả lời sai: Minh được 0 điểm. Cuộc chơi kết thúc tại đây
Khi đó, \(P\left( {Y = 0} \right) = P(\overline B ) = 1--P\left( B \right) = 1--0,6 = 0,4.\)
+ Nếu trả lời đúng Minh nhận 80 điểm và Minh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi loại I. Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi và số điểm với số điểm nhận được là 80 + 0 = 80 điểm. Theo giả thiết A và B là biến cố độc lập. Theo công thức nên xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 80} \right) = P(B\overline A ) = P\left( B \right)P(\overline A ) = \left( {0,6} \right)\left( {1--0,8} \right) = 0,12\)
+ Nếu trả lời đúng Minh nhận 80 điểm. Cuộc chơi kết thúc tại đây và Minh được 20 + 80 = 100 điểm. Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 100} \right) = P\left( {BA} \right) = P\left( B \right)P\left( A \right) = 0,6.{\rm{ }}0,8 = 0,48\)
Bảng phân bố xác suất của Y là:
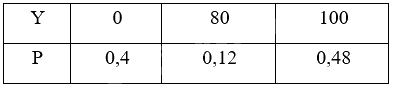
Ta có: \(E\left( Y \right) = 0.0,4 + 80.0,12 + 100.0,48 = 57,6\).
Vậy trung bình Minh được 57,6 điểm
b) Ta có \(E(X) = 54,4\), \(E(Y) = 57,6\). Ta thấy \(E(Y) > E(X)\) nên ở vòng 1, Minh nên chọn câu hỏi loại II.
Trả lời câu hỏi Hoạt động 4 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Một nhà đầu tư xem xét hai phương án đầu tư. Với phương án 1 thì doanh thu một năm sẽ là 8 tỉ đồng hoặc 2 tỉ đồng với xác suất tương ứng là \(\frac{1}{3}\) và \(\frac{2}{3}\). Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau.
a) Hãy so sánh doanh thu trung bình của phương án 1 và phương án 2.
b) Nhà đầu tư nên chọn phương án nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X, Y.
Bước 2: Tính kì vọng \(E(X)\),\(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2
Ta có bảng phân bố xác suất của biến ngẫu nhiên X và Y

Khi đó, \(E(X) = 8.\frac{1}{3} + 2.\frac{2}{3} = 4\); \(E(Y) = 3.\frac{1}{2} + 5.\frac{1}{2} = 4\).
Ta thấy \(E(X) = E(Y)\) nên doanh thu trung bình của hai phương án bằng nhau.
b)
Phương án 1 nếu nhà đầu tư ưa mạo hiểm
Phương án 2 nếu nhà đầu tư muốn sự an toàn
Trả lời câu hỏi Luyện tập 3 trang 12 Chuyên đề học tập Toán 12 Kết nối tri thức
Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:

a) Tính \(V(X)\) và \(\sigma (X)\) theo định nghĩa
b) Tính \(V(X)\) theo công thức (2).
Phương pháp giải:
Áp dụng các công thức để tính.
Lời giải chi tiết:
a)
\(E(X) = 0.0,16 + 1.0,18 + 2.0,25 + 3.0,28 + 4.0,13 = 2,04.\)
\(\begin{array}{l}V\left( X \right) = {\left( {0--2,04} \right)^2}.0,16 + {\left( {1--2,04} \right)^2}.0,18 + {\left( {2--2,04} \right)^2}.0,25 + {\left( {3--2,04} \right)^2}.0,28\\{\rm{ }} + {\left( {4--2,04} \right)^2}.0,13 = 1,6184.\\ \Rightarrow \sigma \left( X \right) = \sqrt {1,6184} \approx 1,2722\end{array}\)
b) \(V\left( X \right) = {0^2}.0,16 + {1^2}.0,18 + {2^2}.0,25 + {3^2}.0,28 + {4^2}.0,13--{\left( {2,04} \right)^2} = 1,6184.\)
Trả lời câu hỏi Hoạt động 3 trang 9 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường AB trong 98 buổi tối thứ Bảy được thống kê như sau: 10 tối không có vụ nào; 20 tối có 1 vụ; 23 tối có 2 vụ; 25 tối có 3 vụ; 15 tối có 4 vụ; 5 tối có 7 vụ. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường B trong 98 buổi tối thứ Bảy đó?
Phương pháp giải:
Trung bình = Tổng số vụ tai nạn / số buổi tối thứ Bảy
Lời giải chi tiết:
Có: \(0.10 + 1.20 + 2.23 + 3.25 + 4.15 + 7.5 = 236\) vụ vi phạm trong 98 buổi tối thứ Bảy
Vậy trung bình có \(\frac{{236}}{{98}} \approx 2,408\) vụ vi phạm trọng 98 buổi tối thứ Bảy
Trả lời câu hỏi Luyện tập 2 trang 10 Chuyên đề học tập Toán 12 Kết nối tri thức
Giả sử số vụ vi phạm Luật Giao thông trên một đoạn đường vào tối thứ Bảy có thể là 0; 1; 2; 3; 4; 5 với các xác suất tương ứng là 0,1; 0,2; 0,25; 0,15 và 0,05. Hỏi trung bình có bao nhiêu vụ vi phạm Luật Giao thông trên đoạn đường đó và tối thứ Bảy?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X
Bước 2: Tính kì vọng \(E(X)\) theo công thức
Lời giải chi tiết:
Gọi X là số vụ vi phạm Luật Giao thông đường bộ trên đoạn đường vào tối thứ Bảy. Khi đó, X là biến ngẫu nhiên rời rạc có bảng phân bố xác suất:

Ta có:
\(\;E(X) = 0,01 + 1.0,2 + 2.0,25 + 3.0,25 + 4.0,15 + 5.0,05 = 2,3\)
Vậy trên đoạn đường vào tối thứ Bảy có trung bình 2,3 vụ vi phạm Luật Giao thông đường bộ
Trả lời câu hỏi Vận dụng 2 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Tiếp tục xét tình huống mở đầu, giả sử ở vòng 1 Minh chọn câu hỏi loại II.
a) Hỏi trung bình Minh nhận được bao nhiêu điểm?
b) Ở vòng 1 Minh nên chọn loại câu hỏi nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên Y.
Bước 2: Tính kì vọng \(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Giả sử ở vòng 1 Minh chọn câu hỏi loại II. Gọi Y là số điểm Minh nhận được.
Gọi A là biến cố “Minh trả lời đúng câu hỏi loại I” \( \Rightarrow P\left( A \right) = 0,8\)
B là biến cố “Minh trả lời đúng câu hỏi loại II”. \( \Rightarrow P\left( B \right) = 0,6\)
+ Nếu trả lời sai: Minh được 0 điểm. Cuộc chơi kết thúc tại đây
Khi đó, \(P\left( {Y = 0} \right) = P(\overline B ) = 1--P\left( B \right) = 1--0,6 = 0,4.\)
+ Nếu trả lời đúng Minh nhận 80 điểm và Minh sẽ bước vào vòng 2, bốc ngẫu nhiên một câu hỏi loại I. Nếu trả lời sai, Minh không có điểm và phải dừng cuộc chơi và số điểm với số điểm nhận được là 80 + 0 = 80 điểm. Theo giả thiết A và B là biến cố độc lập. Theo công thức nên xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 80} \right) = P(B\overline A ) = P\left( B \right)P(\overline A ) = \left( {0,6} \right)\left( {1--0,8} \right) = 0,12\)
+ Nếu trả lời đúng Minh nhận 80 điểm. Cuộc chơi kết thúc tại đây và Minh được 20 + 80 = 100 điểm. Theo công thức nhân xác suất cho hai biến cố độc lập ta có:
\(P\left( {Y = 100} \right) = P\left( {BA} \right) = P\left( B \right)P\left( A \right) = 0,6.{\rm{ }}0,8 = 0,48\)
Bảng phân bố xác suất của Y là:
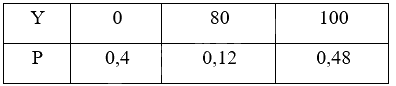
Ta có: \(E\left( Y \right) = 0.0,4 + 80.0,12 + 100.0,48 = 57,6\).
Vậy trung bình Minh được 57,6 điểm
b) Ta có \(E(X) = 54,4\), \(E(Y) = 57,6\). Ta thấy \(E(Y) > E(X)\) nên ở vòng 1, Minh nên chọn câu hỏi loại II.
Trả lời câu hỏi Hoạt động 4 trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Một nhà đầu tư xem xét hai phương án đầu tư. Với phương án 1 thì doanh thu một năm sẽ là 8 tỉ đồng hoặc 2 tỉ đồng với xác suất tương ứng là \(\frac{1}{3}\) và \(\frac{2}{3}\). Với phương án 2 thì doanh thu một năm sẽ là 5 tỉ đồng hoặc 3 tỉ đồng với hai xác suất bằng nhau.
a) Hãy so sánh doanh thu trung bình của phương án 1 và phương án 2.
b) Nhà đầu tư nên chọn phương án nào?
Phương pháp giải:
Bước 1: Dựa vào dữ kiện đề bài lập bảng phân bố xác suất của biến ngẫn nhiên X, Y.
Bước 2: Tính kì vọng \(E(X)\),\(E(Y)\) theo công thức.
Bước 3: So sánh \(E(X)\) với \(E(Y)\) và đưa ra kết luận.
Lời giải chi tiết:
a) Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2
Ta có bảng phân bố xác suất của biến ngẫu nhiên X và Y

Khi đó, \(E(X) = 8.\frac{1}{3} + 2.\frac{2}{3} = 4\); \(E(Y) = 3.\frac{1}{2} + 5.\frac{1}{2} = 4\).
Ta thấy \(E(X) = E(Y)\) nên doanh thu trung bình của hai phương án bằng nhau.
b)
Phương án 1 nếu nhà đầu tư ưa mạo hiểm
Phương án 2 nếu nhà đầu tư muốn sự an toàn
Trả lời câu hỏi trang 11 Chuyên đề học tập Toán 12 Kết nối tri thức
Trở lại HĐ4. Gọi X và Y tương ứng là doanh thu theo phương án 1 và phương án 2. Tính độ lệch chuẩn của X và Y.
Phương pháp giải:
Áp dụng công thức tính độ lệch chuẩn
Lời giải chi tiết:
\(\begin{array}{l}E(X) = 4\\V(X) = {\left( {8 - 4} \right)^2}.\frac{1}{3} + {\left( {2 - 4} \right)^2}.\frac{2}{3} = 8\\ \Rightarrow \sigma (X) = \sqrt 8 \approx 2,828.\end{array}\)
\(\begin{array}{l}E(Y) = 4\\V\left( Y \right) = {\left( {5 - 4} \right)^2}.\frac{1}{2} + {\left( {3 - 4} \right)^2}.\frac{1}{2} = 1\\ \Rightarrow \sigma \left( Y \right) = 1\end{array}\)
Trả lời câu hỏi Luyện tập 3 trang 12 Chuyên đề học tập Toán 12 Kết nối tri thức
Cho biến ngẫu nhiên rời rạc X với bảng phân bố xác suất như sau:

a) Tính \(V(X)\) và \(\sigma (X)\) theo định nghĩa
b) Tính \(V(X)\) theo công thức (2).
Phương pháp giải:
Áp dụng các công thức để tính.
Lời giải chi tiết:
a)
\(E(X) = 0.0,16 + 1.0,18 + 2.0,25 + 3.0,28 + 4.0,13 = 2,04.\)
\(\begin{array}{l}V\left( X \right) = {\left( {0--2,04} \right)^2}.0,16 + {\left( {1--2,04} \right)^2}.0,18 + {\left( {2--2,04} \right)^2}.0,25 + {\left( {3--2,04} \right)^2}.0,28\\{\rm{ }} + {\left( {4--2,04} \right)^2}.0,13 = 1,6184.\\ \Rightarrow \sigma \left( X \right) = \sqrt {1,6184} \approx 1,2722\end{array}\)
b) \(V\left( X \right) = {0^2}.0,16 + {1^2}.0,18 + {2^2}.0,25 + {3^2}.0,28 + {4^2}.0,13--{\left( {2,04} \right)^2} = 1,6184.\)
Mục 2 của Chuyên đề học tập Toán 12 - Kết nối tri thức tập trung vào các kiến thức về đạo hàm của hàm số. Đây là một phần quan trọng trong chương trình Toán 12, đóng vai trò nền tảng cho việc giải quyết các bài toán liên quan đến cực trị, đơn điệu và ứng dụng của đạo hàm trong thực tế. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là điều cần thiết để đạt kết quả tốt trong kỳ thi THPT Quốc gia.
Chúng ta sẽ cùng nhau đi sâu vào giải chi tiết từng bài tập trong mục 2, trang 9, 10, 11, 12. Mỗi bài tập sẽ được phân tích kỹ lưỡng, từ việc xác định đúng công thức đạo hàm cần sử dụng đến việc trình bày lời giải một cách logic và dễ hiểu.
Các bài tập trên trang 9 thường tập trung vào việc tính đạo hàm của các hàm số đơn giản như hàm đa thức, hàm lượng giác và hàm mũ. Để giải quyết các bài tập này, các em cần nắm vững các công thức đạo hàm cơ bản và áp dụng chúng một cách linh hoạt.
Trang 10 giới thiệu các bài tập về đạo hàm của hàm hợp. Để giải quyết các bài tập này, các em cần áp dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Ví dụ: Cho hàm số y = sin(x2). Để tính đạo hàm của hàm số này, ta đặt u(v) = sin(v) và v(x) = x2. Khi đó, y' = cos(x2) * 2x.
Các bài tập trên trang 11 và 12 thường là sự kết hợp của nhiều kiến thức và kỹ năng khác nhau. Các em cần vận dụng linh hoạt các công thức đạo hàm, quy tắc đạo hàm và các kỹ năng biến đổi đại số để giải quyết các bài tập này.
Một số dạng bài tập thường gặp trên trang 11 và 12 bao gồm:
Để giải bài tập Toán 12 Chuyên đề học tập - Kết nối tri thức một cách hiệu quả, các em nên:
Hy vọng rằng với những hướng dẫn chi tiết và lời giải đầy đủ trên đây, các em sẽ tự tin hơn trong việc giải bài tập mục 2 trang 9, 10, 11, 12 Chuyên đề học tập Toán 12 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi THPT Quốc gia!