Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 12 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 của Chuyên đề học tập Toán 12 - Kết nối tri thức, cụ thể là các trang 17, 18, 19 và 20.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.
Cho T là một phép thử và E là một biến cố liên quan tới phép thử T. Ta thực hiện phép thử T lặp lại n lần một cách độc lập. Ở mỗi lần thực hiện phép thử T, biến cố E có xác suất xuất hiện bằng p, tức là \(P\left( E \right) = p\), 0 < p < 1. Gọi X là số lần xuất hiện biến cố E trong n lần thực hiện lặp lại phép thử T. Tính \(P\left( {X = k} \right)\) với k ∈ {0; 1; …; n}.
Trả lời câu hỏi Hoạt động 2 trang 17 Chuyên đề học tập Toán 12 Kết nối tri thức
Cho T là một phép thử và E là một biến cố liên quan tới phép thử T. Ta thực hiện phép thử T lặp lại n lần một cách độc lập. Ở mỗi lần thực hiện phép thử T, biến cố E có xác suất xuất hiện bằng p, tức là \(P\left( E \right) = p\), 0 < p < 1. Gọi X là số lần xuất hiện biến cố E trong n lần thực hiện lặp lại phép thử T. Tính \(P\left( {X = k} \right)\) với k ∈ {0; 1; …; n}.
Phương pháp giải:
Sử dụng công thức Bernoulli
Lời giải chi tiết:
Biến cố \(\left\{ {X = k} \right\}\) là: “ Trong \(n\) lần thực hiện phép thử T, biến cố E xuất hiện đúng \(k\) lần”
Vậy \(P(X = k)\) là xác suất để trong \(n\) lần thực hiện phép thử T, biến cố E xuất hiện đúng \(k\) lần. Theo công thức Bernoulli ta có \(P(X = k) = C_n^k.{p^k}.{(1 - p)^{n - k}}\)
Trả lời câu hỏi Vận dụng trang 20 Chuyên đề học tập Toán 12 Kết nối tri thức
Giải quyết bài toán ở tình huống mở đầu.
Phương pháp giải:
Áp dụng phân bố nhị thức và công thức tính kì vọng của biến ngẫu nhiên có phân bố nhị thức
Lời giải chi tiết:
Gọi X là số câu trả lời đúng của An. Khi đó \(X \sim B(10;0,25)\)
Số điểm trung bình là \(E\left( X \right)\).
Vậy trung bình An nhận được số điểm trung bình là:
\(E(X) = 10.0,25 = 2,5\) (Điểm)
b) An vượt qua bài thi khi làm đúng ít nhất 5 câu tức là khi X ≥ 5.
Theo chú ý về phân bố nhị thức ta có:
\(\begin{array}{l}P(X \ge 5) = P(X = 5) + P(X = 6) + ... + P(X = 10)\\{\rm{ = }}C_{10}^5.{\left( {\frac{1}{4}} \right)^5}.{\left( {\frac{3}{4}} \right)^5} + C_{10}^6.{\left( {\frac{1}{4}} \right)^6}.{\left( {\frac{3}{4}} \right)^4} + ... + C_{10}^{10}.{\left( {\frac{1}{4}} \right)^{10}}.{\left( {\frac{3}{4}} \right)^0}{\rm{ = }}0,0781\end{array}\)
Trả lời câu hỏi Luyện tập 3 trang 18 Chuyên đề học tập Toán 12 Kết nối tri thức
Khi tham gia một một trò chơi, người chơi gieo xúc xắc cân đối, đồng chất một cách độc lập liên tiếp 5 lần. Mỗi lần gieo nếu số chấm xuất hiện lớn hơn 4 thì người chơi được 10 điểm. Tính xác suất để người chơi nhận được ít nhất 30 điểm.
Phương pháp giải:
Áp dụng phân bố nhị thức để giải bài tập.
Lời giải chi tiết:
Phép thử T là: “Gieo một con xúc xắc cân đối, đồng chất”.
Biến cố E: “Số chấm xuất hiện lớn hơn 4”. \( \Rightarrow P(E) = \frac{1}{3}\)
X là số lần xuất hiện biến cố E trong 5 lần thực hiện lặp lại phép thử T.
Khi đó \(X \sim B\left( {5;\frac{1}{3}} \right)\)
Người chơi nhận được ít nhất 30 điểm khi số lần xuất hiện số chấm lớn hơn 4 ít nhất 3 lần. Vậy người chơi nhận được ít nhất 30 điểm khi \(X \ge 3\).
\(\begin{array}{l}P(X \ge 3) = P(X = 3) + P(X = 4) + P(X = 5)\\{\rm{ = }}C_5^3.{\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{2}{3}} \right)^2} + C_5^4.{\left( {\frac{1}{3}} \right)^4}.{\left( {\frac{2}{3}} \right)^1} + C_5^5.{\left( {\frac{1}{3}} \right)^5}.{\left( {\frac{2}{3}} \right)^0} \approx 0,21\end{array}\)
Trả lời câu hỏi trang 17 Chuyên đề học tập Toán 12 Kết nối tri thức
Viết bảng phân bố xác suất của biến ngẫu nhiên có phân bố Bernoulli
Phương pháp giải:
Dựa vào khái niệm biến ngẫu nhiên có phân bố Bernoulli.
Lời giải chi tiết:
Gọi X là biến ngẫu nhiên có phân bố Bernoulli \( \Rightarrow X \sim Ber(p)\)
Các giá trị của X có thể nhận được thuộc tập {0; 1}.
\(\begin{array}{l}P(X = 0) = C_1^0.{p^0}.{(1 - p)^{1 - 0}} = 1 - p\\P(X = 1) = C_1^1.{p^1}.{(1 - p)^{1 - 1}} = p\end{array}\)
Ta có bảng bảng phân bố xác suất của biến ngẫu nhiên X:
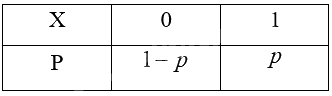
Trả lời câu hỏi Hoạt động 2 trang 17 Chuyên đề học tập Toán 12 Kết nối tri thức
Cho T là một phép thử và E là một biến cố liên quan tới phép thử T. Ta thực hiện phép thử T lặp lại n lần một cách độc lập. Ở mỗi lần thực hiện phép thử T, biến cố E có xác suất xuất hiện bằng p, tức là \(P\left( E \right) = p\), 0 < p < 1. Gọi X là số lần xuất hiện biến cố E trong n lần thực hiện lặp lại phép thử T. Tính \(P\left( {X = k} \right)\) với k ∈ {0; 1; …; n}.
Phương pháp giải:
Sử dụng công thức Bernoulli
Lời giải chi tiết:
Biến cố \(\left\{ {X = k} \right\}\) là: “ Trong \(n\) lần thực hiện phép thử T, biến cố E xuất hiện đúng \(k\) lần”
Vậy \(P(X = k)\) là xác suất để trong \(n\) lần thực hiện phép thử T, biến cố E xuất hiện đúng \(k\) lần. Theo công thức Bernoulli ta có \(P(X = k) = C_n^k.{p^k}.{(1 - p)^{n - k}}\)
Trả lời câu hỏi trang 17 Chuyên đề học tập Toán 12 Kết nối tri thức
Viết bảng phân bố xác suất của biến ngẫu nhiên có phân bố Bernoulli
Phương pháp giải:
Dựa vào khái niệm biến ngẫu nhiên có phân bố Bernoulli.
Lời giải chi tiết:
Gọi X là biến ngẫu nhiên có phân bố Bernoulli \( \Rightarrow X \sim Ber(p)\)
Các giá trị của X có thể nhận được thuộc tập {0; 1}.
\(\begin{array}{l}P(X = 0) = C_1^0.{p^0}.{(1 - p)^{1 - 0}} = 1 - p\\P(X = 1) = C_1^1.{p^1}.{(1 - p)^{1 - 1}} = p\end{array}\)
Ta có bảng bảng phân bố xác suất của biến ngẫu nhiên X:
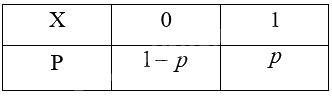
Trả lời câu hỏi Luyện tập 3 trang 18 Chuyên đề học tập Toán 12 Kết nối tri thức
Khi tham gia một một trò chơi, người chơi gieo xúc xắc cân đối, đồng chất một cách độc lập liên tiếp 5 lần. Mỗi lần gieo nếu số chấm xuất hiện lớn hơn 4 thì người chơi được 10 điểm. Tính xác suất để người chơi nhận được ít nhất 30 điểm.
Phương pháp giải:
Áp dụng phân bố nhị thức để giải bài tập.
Lời giải chi tiết:
Phép thử T là: “Gieo một con xúc xắc cân đối, đồng chất”.
Biến cố E: “Số chấm xuất hiện lớn hơn 4”. \( \Rightarrow P(E) = \frac{1}{3}\)
X là số lần xuất hiện biến cố E trong 5 lần thực hiện lặp lại phép thử T.
Khi đó \(X \sim B\left( {5;\frac{1}{3}} \right)\)
Người chơi nhận được ít nhất 30 điểm khi số lần xuất hiện số chấm lớn hơn 4 ít nhất 3 lần. Vậy người chơi nhận được ít nhất 30 điểm khi \(X \ge 3\).
\(\begin{array}{l}P(X \ge 3) = P(X = 3) + P(X = 4) + P(X = 5)\\{\rm{ = }}C_5^3.{\left( {\frac{1}{3}} \right)^3}.{\left( {\frac{2}{3}} \right)^2} + C_5^4.{\left( {\frac{1}{3}} \right)^4}.{\left( {\frac{2}{3}} \right)^1} + C_5^5.{\left( {\frac{1}{3}} \right)^5}.{\left( {\frac{2}{3}} \right)^0} \approx 0,21\end{array}\)
Trả lời câu hỏi Vận dụng trang 20 Chuyên đề học tập Toán 12 Kết nối tri thức
Giải quyết bài toán ở tình huống mở đầu.
Phương pháp giải:
Áp dụng phân bố nhị thức và công thức tính kì vọng của biến ngẫu nhiên có phân bố nhị thức
Lời giải chi tiết:
Gọi X là số câu trả lời đúng của An. Khi đó \(X \sim B(10;0,25)\)
Số điểm trung bình là \(E\left( X \right)\).
Vậy trung bình An nhận được số điểm trung bình là:
\(E(X) = 10.0,25 = 2,5\) (Điểm)
b) An vượt qua bài thi khi làm đúng ít nhất 5 câu tức là khi X ≥ 5.
Theo chú ý về phân bố nhị thức ta có:
\(\begin{array}{l}P(X \ge 5) = P(X = 5) + P(X = 6) + ... + P(X = 10)\\{\rm{ = }}C_{10}^5.{\left( {\frac{1}{4}} \right)^5}.{\left( {\frac{3}{4}} \right)^5} + C_{10}^6.{\left( {\frac{1}{4}} \right)^6}.{\left( {\frac{3}{4}} \right)^4} + ... + C_{10}^{10}.{\left( {\frac{1}{4}} \right)^{10}}.{\left( {\frac{3}{4}} \right)^0}{\rm{ = }}0,0781\end{array}\)
Mục 2 của Chuyên đề học tập Toán 12 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể trong chương trình Toán 12. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, công thức và phương pháp giải liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trang 17, 18, 19 và 20, đồng thời phân tích các điểm quan trọng cần lưu ý.
Trang 17 thường chứa các bài tập vận dụng kiến thức cơ bản để kiểm tra mức độ hiểu bài của học sinh. Các bài tập này thường liên quan đến việc xác định các yếu tố của hàm số, vẽ đồ thị hàm số hoặc giải các phương trình, bất phương trình đơn giản.
Trang 18 thường chứa các bài tập nâng cao hơn, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học và có khả năng tư duy logic. Các bài tập này có thể liên quan đến việc giải các bài toán thực tế, chứng minh các đẳng thức hoặc tìm các giá trị lớn nhất, nhỏ nhất của hàm số.
Trang 19 tiếp tục cung cấp các bài tập vận dụng và nâng cao, tập trung vào các kỹ năng giải toán phức tạp hơn. Học sinh cần chú ý đến việc phân tích đề bài, lựa chọn phương pháp giải phù hợp và kiểm tra lại kết quả.
Trang 20 thường chứa các bài tập tổng hợp, giúp học sinh củng cố kiến thức và kỹ năng đã học trong mục 2. Các bài tập này có thể kết hợp nhiều kiến thức khác nhau và đòi hỏi học sinh phải có khả năng giải quyết vấn đề một cách sáng tạo.
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 17, 18, 19, 20 Chuyên đề học tập Toán 12 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao!