Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong Chuyên đề học tập Toán 12 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập phức tạp.
Do đó, chúng tôi đã biên soạn bộ giải bài tập này với mục đích giúp các bạn học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.
Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam. Nhà anh ấy nằm bên bờ biển, cách vị trí điểm P khoảng 6 km về phía bắc. Anh ấy có thể chèo thuyền với vận tốc 3 km/h và đi bộ với vận tốc 5 km/h (giả sử vận tốc của dòng nước là không đáng kể so với vận tốc mà người đánh cá chèo thuyền). Anh ấy dự kiến sẽ chèo thuyền thẳng đến một điểm Q đâu đó trên bờ biển về phía bắc điểm P, với 0 ≤ PQ ≤ 6 (km), rồi đi bộ quãng
Trả lời câu hỏi Hoạt động 1 trang 34 Chuyên đề học tập Toán 12 Kết nối tri thức
Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam. Nhà anh ấy nằm bên bờ biển, cách vị trí điểm P khoảng 6 km về phía bắc. Anh ấy có thể chèo thuyền với vận tốc 3 km/h và đi bộ với vận tốc 5 km/h (giả sử vận tốc của dòng nước là không đáng kể so với vận tốc mà người đánh cá chèo thuyền). Anh ấy dự kiến sẽ chèo thuyền thẳng đến một điểm Q đâu đó trên bờ biển về phía bắc điểm P, với 0 ≤ PQ ≤ 6 (km), rồi đi bộ quãng đường còn lại để về nhà.
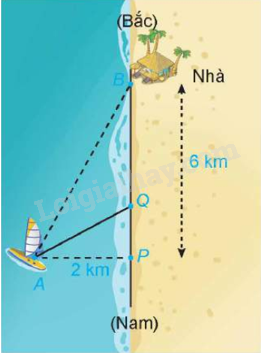
a) Hãy chọn các kí hiệu cho các đại lượng đã biết và đại lượng chưa biết trong bài toán trên.
b) Tìm các mối quan hệ giữa các kí hiệu trong câu a).
c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết bao nhiêu thời gian?
d) Nếu anh ấy chèo thuyền đến điểm Q, rồi đi bộ về nhà thì hết bao nhiêu thời gian?
Phương pháp giải:
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết:
a) Kí hiệu v1 là vận tốc chèo thuyền (v1 = 3 km/h) và v2 là vận tốc đi bộ (v2 = 5 km/h).
Kí hiệu S1, v1 là quãng đường và vận tốc chèo thuyền của người đánh cá khi chèo thuyền.
Kí hiệu S2, v2 là quãng đường và vận tốc của người đánh cá khi đi bộ dọc bờ biển.
Ta có: v1 = 3 km/h, v2 = 5 km/h.
Đặt \(PQ{\rm{ }} = {\rm{ }}x\) (km), \(x \in \left[ {0;6} \right]\).
b) Ta có: \({S_2} = BQ = 6 - x{\rm{ }}(km)\)
Vì tam giác APQ vuông tại P nên \({S_1} = AQ = \sqrt {A{P^2} + P{Q^2}} = \sqrt {4 + {x^2}} .\)
c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết
\(t = {t_{AP}} + {t_{PB}} = \frac{2}{3} + \frac{6}{5} = \frac{{28}}{{15}}\) (giờ)
d) Nếu anh ấy chèo thuyền đến Q rồi đi bộ về nhà thì hết
\(t = {t_{AQ}} + {t_{QB}} = \frac{{\sqrt {4 + {x^2}} }}{3} + \frac{{6 - x}}{5}\) (giờ)
Trả lời câu hỏi Luyện tập 2 trang 38 Chuyên đề học tập Toán 12 Kết nối tri thức
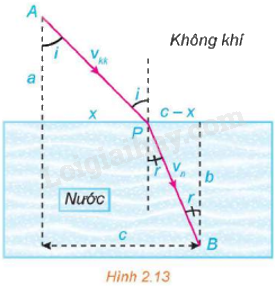
Gọi \({v_{kk}}\) là vận tốc ánh sáng trong không khí và \({v_n}\) là vận tốc ánh sáng trong nước. Theo nguyên lí Fermat, một tia sáng di chuyển từ một điểm A trong không khí đến một điểm B trong nước theo đường gấp khúc APB sao cho tổng thời gian di chuyển là nhỏ nhất (Hình 2.13). Vận dụng đạo hàm tìm vị trí cực trị của hàm số T(x) (tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB) để chứng tỏ rằng khi T(x) nhỏ nhất thì góc tới i và góc khúc xạ r thỏa mãn phương trình \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\).
Phương trình này được gọi là Định luật Snell.
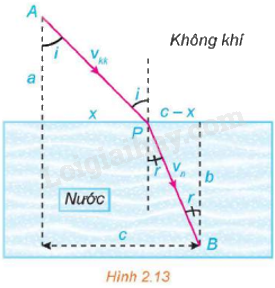
Phương pháp giải:
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết:
Từ hình vẽ, với 0 ≤ x ≤ c ta có: \(AP = \sqrt {{a^2} + {x^2}} \) và \(PB = \sqrt {{b^2} + {{(c - x)}^2}} .\)
Thời gian ánh sáng di chuyển từ A đến P là: \({t_1} = \frac{{AP}}{{{v_{kk}}}} = \frac{{\sqrt {{a^2} + {x^2}} }}{{{v_{kk}}}}.\) .
Thời gian ánh sáng di chuyển từ P đến B là: \({t_2} = \frac{{PB}}{{{v_n}}} = \frac{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}{{{v_n}}}.\)
Khi đó, tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB là:
\(T\left( x \right) = {t_1} + {t_2} = \frac{{\sqrt {{a^2} + {x^2}} }}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}{{{v_n}}},0 \le x \le c.\)
Đạo hàm của hàm T(x) là: \(T'\left( x \right) = \frac{x}{{{v_{kk}}\sqrt {{a^2} + {x^2}} }} - \frac{{c - x}}{{{v_n}\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}.\)
Ta có
\(\begin{array}{l}T'\left( x \right) = 0 \Leftrightarrow \frac{x}{{{v_{kk}}\sqrt {{a^2} + {x^2}} }} = \frac{{c - x}}{{{v_n}\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}.\\ \Leftrightarrow \frac{1}{{{v_{kk}}}} \cdot \frac{x}{{\sqrt {{a^2} + {x^2}} }} = \frac{1}{{{v_n}}} \cdot \frac{{c - x}}{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}\\ \Leftrightarrow \frac{1}{{{v_{kk}}}}\sin i = \frac{1}{{{v_n}}}\sin r \Leftrightarrow \frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}.\end{array}\)
Giả sử x = x0 thỏa mãn \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\)
Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:
\(T\left( 0 \right) = \frac{a}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {c^2}} }}{{{v_n}}};\,\,T\left( {{x_0}} \right) = \frac{{\sqrt {{a^2} + x_0^2} }}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {{\left( {c - {x_0}} \right)}^2}} }}{{{v_n}}};\,\,T\left( c \right) = \frac{{\sqrt {{a^2} + {c^2}} }}{{{v_{kk}}}} + \frac{b}{{{v_n}}}.\)
Ta có T(x0) là giá trị nhỏ nhất trong các giá trị T(0), T(x0), T(c).
Vậy T(x) nhỏ nhất khi góc tới i và góc khúc xạ r thỏa mãn phương trình \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\).
Trả lời câu hỏi Luyện tập 1 trang 37 Chuyên đề học tập Toán 12 Kết nối tri thức
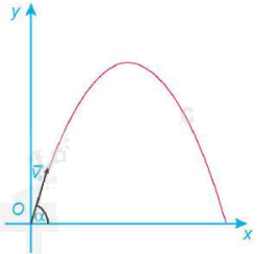
Một vật được ném từ mặt đất lên trời xiên góc \(\alpha \) với phương nằm ngang với vận tốc ban đầu \({v_0}\; = 9{\rm{ }}m/s\)(Hình 2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) , ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).
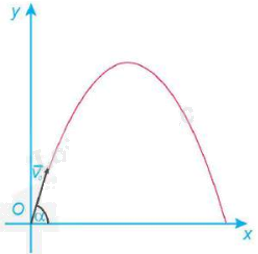
a) Tính độ cao nhất của vật trên quỹ đạo và xác định thời điểm mà vật đạt được độ cao đó (giả sử gia tốc trọng trường là g = 9,8 m/s2).
b) Xác định góc ném α để tầm ném xa của vật đạt giá trị lớn nhất.
Phương pháp giải:
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết:
a) Vì quỹ đạo chuyển động của vật có dạng hàm số bậc 2 đối với biến x có đồ thị là một parabol có bề lõi quay xuống dưới. Độ cao nhất của vật trên quỹ đạo ứng với tung độ đỉnh cao nhất của parabol
Khi đó: \({x_p} = \frac{{ - \tan \alpha }}{{2.\frac{{ - g}}{{2.v_0^2{\rm{co}}{{\rm{s}}^2}\alpha }}}} = \sin \alpha .\cos \alpha .\frac{{v_0^2}}{g};{y_P} = {\sin ^2}\alpha .\frac{{v_0^2}}{{2g}}\)
Tại \({v_0} = 9\)(m/s), ta có độ cao lớn nhất của vật là: \({y_P} = {\sin ^2}\alpha .\frac{{405}}{{98}}\)
Thời điểm vật đạt được độ cao lớn nhất là: \(t = \frac{{{x_p}}}{{{v_0}.\cos \alpha }} = \frac{{{v_0}}}{g}\sin \alpha = \frac{{45}}{{49}}\sin \alpha \)
b) Tầm ném xa trong chuyển động ném xiên là:
\(L = 2{x_p} = \sin 2\alpha .\frac{{v_0^2}}{g} = \frac{{810}}{{98}}\sin 2\alpha \le \frac{{405}}{{49}}\).
Tầm ném xa đạt giá trị lớn nhất bằng \(\frac{{405}}{{49}}\) khi \(\sin 2\alpha = 1\) hay \(\alpha = \frac{\pi }{4}\).
Trả lời câu hỏi Hoạt động 1 trang 34 Chuyên đề học tập Toán 12 Kết nối tri thức
Một người đánh cá đang ở trên thuyền (vị trí A) cách bờ biển (điểm P) 2 km về phía đông trên đường bờ biển thẳng theo phương bắc nam. Nhà anh ấy nằm bên bờ biển, cách vị trí điểm P khoảng 6 km về phía bắc. Anh ấy có thể chèo thuyền với vận tốc 3 km/h và đi bộ với vận tốc 5 km/h (giả sử vận tốc của dòng nước là không đáng kể so với vận tốc mà người đánh cá chèo thuyền). Anh ấy dự kiến sẽ chèo thuyền thẳng đến một điểm Q đâu đó trên bờ biển về phía bắc điểm P, với 0 ≤ PQ ≤ 6 (km), rồi đi bộ quãng đường còn lại để về nhà.
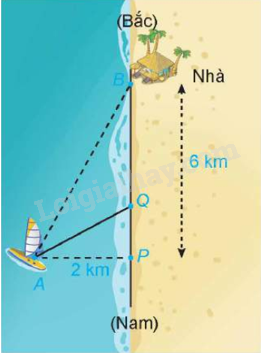
a) Hãy chọn các kí hiệu cho các đại lượng đã biết và đại lượng chưa biết trong bài toán trên.
b) Tìm các mối quan hệ giữa các kí hiệu trong câu a).
c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết bao nhiêu thời gian?
d) Nếu anh ấy chèo thuyền đến điểm Q, rồi đi bộ về nhà thì hết bao nhiêu thời gian?
Phương pháp giải:
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết:
a) Kí hiệu v1 là vận tốc chèo thuyền (v1 = 3 km/h) và v2 là vận tốc đi bộ (v2 = 5 km/h).
Kí hiệu S1, v1 là quãng đường và vận tốc chèo thuyền của người đánh cá khi chèo thuyền.
Kí hiệu S2, v2 là quãng đường và vận tốc của người đánh cá khi đi bộ dọc bờ biển.
Ta có: v1 = 3 km/h, v2 = 5 km/h.
Đặt \(PQ{\rm{ }} = {\rm{ }}x\) (km), \(x \in \left[ {0;6} \right]\).
b) Ta có: \({S_2} = BQ = 6 - x{\rm{ }}(km)\)
Vì tam giác APQ vuông tại P nên \({S_1} = AQ = \sqrt {A{P^2} + P{Q^2}} = \sqrt {4 + {x^2}} .\)
c) Nếu anh ấy chèo thuyền đến P rồi đi bộ về nhà thì hết
\(t = {t_{AP}} + {t_{PB}} = \frac{2}{3} + \frac{6}{5} = \frac{{28}}{{15}}\) (giờ)
d) Nếu anh ấy chèo thuyền đến Q rồi đi bộ về nhà thì hết
\(t = {t_{AQ}} + {t_{QB}} = \frac{{\sqrt {4 + {x^2}} }}{3} + \frac{{6 - x}}{5}\) (giờ)
Trả lời câu hỏi Luyện tập 1 trang 37 Chuyên đề học tập Toán 12 Kết nối tri thức
Một vật được ném từ mặt đất lên trời xiên góc \(\alpha \) với phương nằm ngang với vận tốc ban đầu \({v_0}\; = 9{\rm{ }}m/s\)(Hình 2.10). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) , ở đó x (mét) là khoảng cách vật bay được theo phương ngang từ điểm ném, y (mét) là độ cao so với mặt đất của vật trong quá trình bay, g là gia tốc trọng trường (theo Vật lí đại cương, Nhà xuất bản Giáo dục Việt Nam, 2016).
a) Tính độ cao nhất của vật trên quỹ đạo và xác định thời điểm mà vật đạt được độ cao đó (giả sử gia tốc trọng trường là g = 9,8 m/s2).
b) Xác định góc ném α để tầm ném xa của vật đạt giá trị lớn nhất.
Phương pháp giải:
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết:
a) Vì quỹ đạo chuyển động của vật có dạng hàm số bậc 2 đối với biến x có đồ thị là một parabol có bề lõi quay xuống dưới. Độ cao nhất của vật trên quỹ đạo ứng với tung độ đỉnh cao nhất của parabol
Khi đó: \({x_p} = \frac{{ - \tan \alpha }}{{2.\frac{{ - g}}{{2.v_0^2{\rm{co}}{{\rm{s}}^2}\alpha }}}} = \sin \alpha .\cos \alpha .\frac{{v_0^2}}{g};{y_P} = {\sin ^2}\alpha .\frac{{v_0^2}}{{2g}}\)
Tại \({v_0} = 9\)(m/s), ta có độ cao lớn nhất của vật là: \({y_P} = {\sin ^2}\alpha .\frac{{405}}{{98}}\)
Thời điểm vật đạt được độ cao lớn nhất là: \(t = \frac{{{x_p}}}{{{v_0}.\cos \alpha }} = \frac{{{v_0}}}{g}\sin \alpha = \frac{{45}}{{49}}\sin \alpha \)
b) Tầm ném xa trong chuyển động ném xiên là:
\(L = 2{x_p} = \sin 2\alpha .\frac{{v_0^2}}{g} = \frac{{810}}{{98}}\sin 2\alpha \le \frac{{405}}{{49}}\).
Tầm ném xa đạt giá trị lớn nhất bằng \(\frac{{405}}{{49}}\) khi \(\sin 2\alpha = 1\) hay \(\alpha = \frac{\pi }{4}\).
Trả lời câu hỏi Luyện tập 2 trang 38 Chuyên đề học tập Toán 12 Kết nối tri thức
Gọi \({v_{kk}}\) là vận tốc ánh sáng trong không khí và \({v_n}\) là vận tốc ánh sáng trong nước. Theo nguyên lí Fermat, một tia sáng di chuyển từ một điểm A trong không khí đến một điểm B trong nước theo đường gấp khúc APB sao cho tổng thời gian di chuyển là nhỏ nhất (Hình 2.13). Vận dụng đạo hàm tìm vị trí cực trị của hàm số T(x) (tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB) để chứng tỏ rằng khi T(x) nhỏ nhất thì góc tới i và góc khúc xạ r thỏa mãn phương trình \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\).
Phương trình này được gọi là Định luật Snell.
Phương pháp giải:
Giải theo 5 bước giải bài toán tối ưu bằng cách sử dụng đạo hàm.
Lời giải chi tiết:
Từ hình vẽ, với 0 ≤ x ≤ c ta có: \(AP = \sqrt {{a^2} + {x^2}} \) và \(PB = \sqrt {{b^2} + {{(c - x)}^2}} .\)
Thời gian ánh sáng di chuyển từ A đến P là: \({t_1} = \frac{{AP}}{{{v_{kk}}}} = \frac{{\sqrt {{a^2} + {x^2}} }}{{{v_{kk}}}}.\) .
Thời gian ánh sáng di chuyển từ P đến B là: \({t_2} = \frac{{PB}}{{{v_n}}} = \frac{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}{{{v_n}}}.\)
Khi đó, tổng thời gian tia sáng đi từ A đến B theo đường gấp khúc APB là:
\(T\left( x \right) = {t_1} + {t_2} = \frac{{\sqrt {{a^2} + {x^2}} }}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}{{{v_n}}},0 \le x \le c.\)
Đạo hàm của hàm T(x) là: \(T'\left( x \right) = \frac{x}{{{v_{kk}}\sqrt {{a^2} + {x^2}} }} - \frac{{c - x}}{{{v_n}\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}.\)
Ta có
\(\begin{array}{l}T'\left( x \right) = 0 \Leftrightarrow \frac{x}{{{v_{kk}}\sqrt {{a^2} + {x^2}} }} = \frac{{c - x}}{{{v_n}\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}.\\ \Leftrightarrow \frac{1}{{{v_{kk}}}} \cdot \frac{x}{{\sqrt {{a^2} + {x^2}} }} = \frac{1}{{{v_n}}} \cdot \frac{{c - x}}{{\sqrt {{b^2} + {{\left( {c - x} \right)}^2}} }}\\ \Leftrightarrow \frac{1}{{{v_{kk}}}}\sin i = \frac{1}{{{v_n}}}\sin r \Leftrightarrow \frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}.\end{array}\)
Giả sử x = x0 thỏa mãn \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\)
Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:
\(T\left( 0 \right) = \frac{a}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {c^2}} }}{{{v_n}}};\,\,T\left( {{x_0}} \right) = \frac{{\sqrt {{a^2} + x_0^2} }}{{{v_{kk}}}} + \frac{{\sqrt {{b^2} + {{\left( {c - {x_0}} \right)}^2}} }}{{{v_n}}};\,\,T\left( c \right) = \frac{{\sqrt {{a^2} + {c^2}} }}{{{v_{kk}}}} + \frac{b}{{{v_n}}}.\)
Ta có T(x0) là giá trị nhỏ nhất trong các giá trị T(0), T(x0), T(c).
Vậy T(x) nhỏ nhất khi góc tới i và góc khúc xạ r thỏa mãn phương trình \(\frac{{\sin i}}{{\sin r}} = \frac{{{v_{kk}}}}{{{v_n}}}\).
Mục 1 của Chuyên đề học tập Toán 12 - Kết nối tri thức thường tập trung vào một chủ đề quan trọng, đặt nền móng cho các kiến thức tiếp theo. Việc nắm vững nội dung và phương pháp giải các bài tập trong mục này là vô cùng cần thiết. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trang 34, 35, 36, 37, 38, đồng thời phân tích các kiến thức liên quan và gợi ý phương pháp tiếp cận hiệu quả.
Các bài tập trang 34 thường xoay quanh việc ôn tập kiến thức cơ bản và áp dụng vào các bài toán đơn giản. Chúng ta sẽ bắt đầu với việc nhắc lại các định nghĩa, tính chất quan trọng, sau đó đi vào giải từng bài tập một cách chi tiết, kèm theo các bước thực hiện rõ ràng.
Trang 35 thường nâng cao độ khó hơn một chút, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học và kết hợp với các kỹ năng giải toán. Chúng ta sẽ tập trung vào việc phân tích đề bài, xác định các yếu tố quan trọng và lựa chọn phương pháp giải phù hợp.
Các bài tập trang 36 có thể liên quan đến các ứng dụng thực tế của kiến thức đã học. Chúng ta sẽ xem xét các ví dụ cụ thể và giải thích cách áp dụng các công thức, định lý vào các tình huống thực tế.
Trang 37 thường chứa các bài tập tổng hợp, đòi hỏi học sinh phải kết hợp nhiều kiến thức và kỹ năng khác nhau. Chúng ta sẽ chia nhỏ bài toán thành các phần nhỏ hơn, giải quyết từng phần một cách độc lập và sau đó kết hợp lại để tìm ra đáp án cuối cùng.
Trang 38 thường là phần bài tập luyện tập, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Chúng ta sẽ giải một số bài tập tiêu biểu và cung cấp các gợi ý để học sinh tự giải các bài tập còn lại.
Để giải tốt các bài tập trong mục 1, học sinh cần nắm vững các kiến thức sau:
Để học tập hiệu quả môn Toán, học sinh nên:
Bài tập: Giải phương trình 2x + 3 = 7
Lời giải:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải tốt các bài tập trong mục 1 trang 34, 35, 36, 37, 38 Chuyên đề học tập Toán 12 - Kết nối tri thức. Chúc bạn học tập tốt!