Bài 16 thuộc chương trình Toán 3 Kết nối tri thức với cuộc sống, tập trung vào việc giúp học sinh hiểu rõ khái niệm về điểm ở giữa hai điểm khác và trung điểm của đoạn thẳng. Bài học này là nền tảng quan trọng để các em phát triển tư duy hình học và khả năng giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng phần của bài tập, giúp các em học sinh nắm vững kiến thức và tự tin làm bài.
Một cây cầu đá có 11 tảng đá. Chú chuột túi đang ở tảng đá ghi số 1 (như hình vẽ).
Nam có một đoạn dây dài 20 cm. Bạn ấy muốn cắt một đoạn dây dài 5 cm từ đoạn dây ban đầu mà không cần dùng thước có vạch chia xăng-ti-mét. Em hãy giúp Nam tìm một cách làm.
Phương pháp giải:
- Gập sợi dây làm đôi sao cho hai đầu đoạn dây trùng với nhau. Từ đó ta xác định được trung điểm của sợ dây ban đầu.
- Cắt đoạn dây ở vị trí trung điểm ta được 2 đoạn dây có độ dài 10 cm.
- Tiếp tục, gập 1 sợi dây 10 cm làm đôi sao cho hai đầu đoạn dây trùng với nhau.
- Cắt đoạn dây ở vị trí trung điểm ta được 2 đoạn dây có độ dài 5 cm.
Số ?

Một cây cầu đá có 11 tảng đá. Chú chuột túi đang ở tảng đá ghi số 1 (như hình vẽ). Mỗi lần nhảy, chuột túi sẽ nhảy từ một tảng đá sang tảng đá ghi số liền sau nó. Vậy:
Chuột túi cần nhảy thêm ….. lần đế đến được tảng đá chính giữa cây cầu.
Phương pháp giải:
Cây cầu chia thành 10 đoạn bằng nhau ứng với mỗi lần nhảy của chú chuột.
Để đến tảng đá chính giữa cây cầu chuột túi cần nhảy đến tảng đá số 5.
Lời giải chi tiết:
Để đến tảng đá chính giữa cây cầu chuột túi cần nhảy đến tảng đá số 5.
Vậy chuột túi cần nhảy thêm 4 lần đế đến được tảng đá chính giữa cây cầu.
Xác định trung điểm của đoạn thẳng AB và đoạn thẳng AC.

Phương pháp giải:
- Quan sát hình vẽ để xác định độ dài của các đoạn thẳng AB, AC
- Trung điểm đoạn thẳng AB: nằm giữa hai điểm A và B, chia đoạn AB thành 2 phần bằng nhau
- Trung điểm đoạn thẳng AB: nằm giữa hai điểm A và C, chia đoạn AC thành 2 phần bằng nhau
Lời giải chi tiết:
a) Gọi D nằm giữa A và B sao cho AD = DB = 2 cm.
Điểm D là trung điểm của đoạn AB.
b) Gọi E nằm giữa A và B sao cho AE = EC = 5 cm.
Điểm E là trung điểm của đoạn AC.

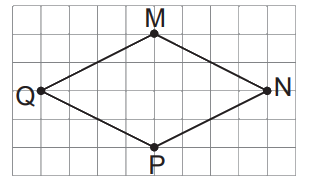
Trong hình vẽ bên, hãy:
a) Vẽ đoạn thẳng MP và vẽ trung điểm A của đoạn thẳng MP.
b) Vẽ đoạn thẳng AN và vẽ trung điểm B của đoạn thẳng AN.
Phương pháp giải:
Quan sát hình vẽ để xác định trung điểm của các đoạn thẳng.
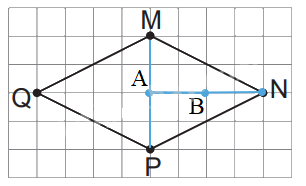
Lời giải chi tiết:
Số ?

Một cây cầu đá có 11 tảng đá. Chú chuột túi đang ở tảng đá ghi số 1 (như hình vẽ). Mỗi lần nhảy, chuột túi sẽ nhảy từ một tảng đá sang tảng đá ghi số liền sau nó. Vậy:
Chuột túi cần nhảy thêm ….. lần đế đến được tảng đá chính giữa cây cầu.
Phương pháp giải:
Cây cầu chia thành 10 đoạn bằng nhau ứng với mỗi lần nhảy của chú chuột.
Để đến tảng đá chính giữa cây cầu chuột túi cần nhảy đến tảng đá số 5.
Lời giải chi tiết:
Để đến tảng đá chính giữa cây cầu chuột túi cần nhảy đến tảng đá số 5.
Vậy chuột túi cần nhảy thêm 4 lần đế đến được tảng đá chính giữa cây cầu.
Nam có một đoạn dây dài 20 cm. Bạn ấy muốn cắt một đoạn dây dài 5 cm từ đoạn dây ban đầu mà không cần dùng thước có vạch chia xăng-ti-mét. Em hãy giúp Nam tìm một cách làm.
Phương pháp giải:
- Gập sợi dây làm đôi sao cho hai đầu đoạn dây trùng với nhau. Từ đó ta xác định được trung điểm của sợ dây ban đầu.
- Cắt đoạn dây ở vị trí trung điểm ta được 2 đoạn dây có độ dài 10 cm.
- Tiếp tục, gập 1 sợi dây 10 cm làm đôi sao cho hai đầu đoạn dây trùng với nhau.
- Cắt đoạn dây ở vị trí trung điểm ta được 2 đoạn dây có độ dài 5 cm.
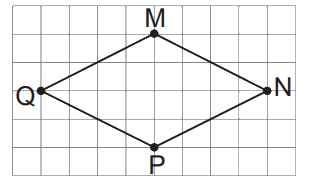
Trong hình vẽ bên, hãy:
a) Vẽ đoạn thẳng MP và vẽ trung điểm A của đoạn thẳng MP.
b) Vẽ đoạn thẳng AN và vẽ trung điểm B của đoạn thẳng AN.
Phương pháp giải:
Quan sát hình vẽ để xác định trung điểm của các đoạn thẳng.
Lời giải chi tiết:
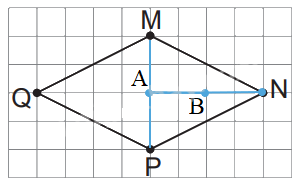
Xác định trung điểm của đoạn thẳng AB và đoạn thẳng AC.

Phương pháp giải:
- Quan sát hình vẽ để xác định độ dài của các đoạn thẳng AB, AC
- Trung điểm đoạn thẳng AB: nằm giữa hai điểm A và B, chia đoạn AB thành 2 phần bằng nhau
- Trung điểm đoạn thẳng AB: nằm giữa hai điểm A và C, chia đoạn AC thành 2 phần bằng nhau
Lời giải chi tiết:
a) Gọi D nằm giữa A và B sao cho AD = DB = 2 cm.
Điểm D là trung điểm của đoạn AB.
b) Gọi E nằm giữa A và B sao cho AE = EC = 5 cm.
Điểm E là trung điểm của đoạn AC.

Bài 16 trong Vở bài tập Toán 3 Kết nối tri thức với cuộc sống tập trung vào việc củng cố kiến thức về điểm ở giữa hai điểm khác và khái niệm trung điểm của một đoạn thẳng. Đây là một bước quan trọng trong việc xây dựng nền tảng hình học cho học sinh lớp 3.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các khái niệm sau:
Bài tập 16 thường bao gồm các dạng bài sau:
Yêu cầu: Cho đoạn thẳng AB và điểm M nằm trên đoạn thẳng đó. Xác định xem M có phải là điểm nằm giữa A và B hay không.
Cách giải: Đo độ dài các đoạn thẳng AM, MB và AB. Nếu AM + MB = AB thì M là điểm nằm giữa A và B.
Yêu cầu: Cho đoạn thẳng AB và điểm M. Xác định xem M có phải là trung điểm của đoạn thẳng AB hay không.
Cách giải: Đo độ dài các đoạn thẳng AM và MB. Nếu AM = MB thì M là trung điểm của đoạn thẳng AB.
Yêu cầu: Vẽ đoạn thẳng AB có độ dài cho trước. Sau đó, xác định trung điểm M của đoạn thẳng AB.
Cách giải: Sử dụng thước kẻ để vẽ đoạn thẳng AB. Sau đó, sử dụng thước kẻ để đo độ dài AB và chia đôi độ dài đó. Đặt điểm M tại vị trí chia đôi đó. Kiểm tra lại bằng cách đo AM và MB để đảm bảo AM = MB.
Để hiểu rõ hơn về bài học, các em có thể luyện tập thêm với các bài tập sau:
Khái niệm về điểm ở giữa và trung điểm của đoạn thẳng là nền tảng quan trọng cho các bài học hình học tiếp theo. Các em cần nắm vững các khái niệm này để có thể giải quyết các bài toán phức tạp hơn.
Ngoài ra, các em có thể tìm hiểu thêm về các loại đoạn thẳng đặc biệt như đoạn thẳng vuông góc, đoạn thẳng song song. Việc hiểu rõ các khái niệm này sẽ giúp các em phát triển tư duy hình học một cách toàn diện.
Bài 16: Điểm ở giữa, trung điểm của đoạn thẳng (tiết 2) trang 45 Vở bài tập Toán 3 - Kết nối tri thức với cuộc sống là một bài học quan trọng giúp học sinh lớp 3 nắm vững các khái niệm cơ bản về hình học. Việc luyện tập thường xuyên và áp dụng kiến thức vào thực tế sẽ giúp các em học tập hiệu quả hơn.
Hy vọng với lời giải chi tiết và các bài tập luyện tập, các em học sinh sẽ tự tin hơn khi giải bài tập Toán 3.