Bài tập phát triển năng lực Toán 4 tập 2 trang 26 phần A là một phần quan trọng giúp học sinh rèn luyện và củng cố kiến thức đã học. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh tự tin giải bài tập.
Chúng tôi không chỉ cung cấp đáp án mà còn giải thích rõ ràng từng bước, giúp các em hiểu bản chất của bài toán và áp dụng vào các bài tập tương tự.
Trong các hình sau, hình nào là hình thoi? Trong hình vẽ bên, em hãy cho biết: a) Tên các cặp cạnh đối diện.
Tính:
\({\text{a) }}\frac{5}{4} \times \frac{2}{3} + \frac{1}{6}{\text{ }}\)
\({\text{b) }}\frac{{17}}{4} - \frac{2}{3}:\frac{1}{6}\)
Phương pháp giải:
Biểu thức có chứa phép cộng, phép trừ, phép nhân, phép chia thì ta thực hiện phép nhân, phép chia trước; thực hiện phép cộng, phép trừ sau.
Lời giải chi tiết:
\({\text{a) }}\frac{5}{4} \times \frac{2}{3} + \frac{1}{6} = \frac{{10}}{{12}} + \frac{1}{6} = \frac{5}{6} + \frac{1}{6} = \frac{6}{6} = 1{\text{ }}\)
\({\text{b) }}\frac{{17}}{4} - \frac{2}{3}:\frac{1}{6} = \frac{{17}}{4} - \frac{2}{3} \times \frac{6}{1} = \frac{{17}}{4} - 4 = \frac{{17}}{4} - \frac{{16}}{4} = \frac{1}{4}{\text{ }}\)
Cho các phân số: $\frac{3}{5};\frac{{32}}{{42}};\frac{{36}}{{60}};\frac{{30}}{{36}};\frac{{15}}{{24}};\frac{{16}}{{21}}.$
a) Rút gọn các phân số chưa tối giản trong các phân số trên.
b) Trong các phân số trên, những phân số bằng nhau là: .......................................................................
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
a) $\frac{{32}}{{42}} = \frac{{32:2}}{{42:2}} = \frac{{16}}{{21}}$
$\frac{{36}}{{60}} = \frac{{36:12}}{{60:12}} = \frac{3}{5}$
$\frac{{30}}{{36}} = \frac{{30:6}}{{36:6}} = \frac{5}{6}$
$\frac{{15}}{{24}} = \frac{{15:3}}{{24:3}} = \frac{5}{8}$
b) Trong các phân số trên, những phân số bằng nhau là: $\frac{3}{5}$và $\frac{{36}}{{60}}$;\(\frac{{32}}{{42}}\) và $\frac{{16}}{{21}}$.
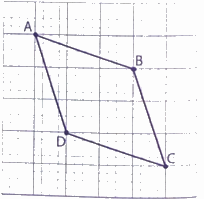
Trong hình vẽ bên, em hãy cho biết:
a) Tên các cặp cạnh đối diện.
b) - Các cặp cạnh đối diện có song song và bằng nhau không?
- Bốn cạnh có bằng nhau không?
Phương pháp giải:
Quan sát hình vẽ và trả lời câu hỏi đề bài.
Lời giải chi tiết:
a) Tên các cặp cạnh đối diện: AB và DC; AD và BC.
b) - Các cặp cạnh đối diện có song song và bằng nhau.
- Bốn cạnh có bằng nhau.
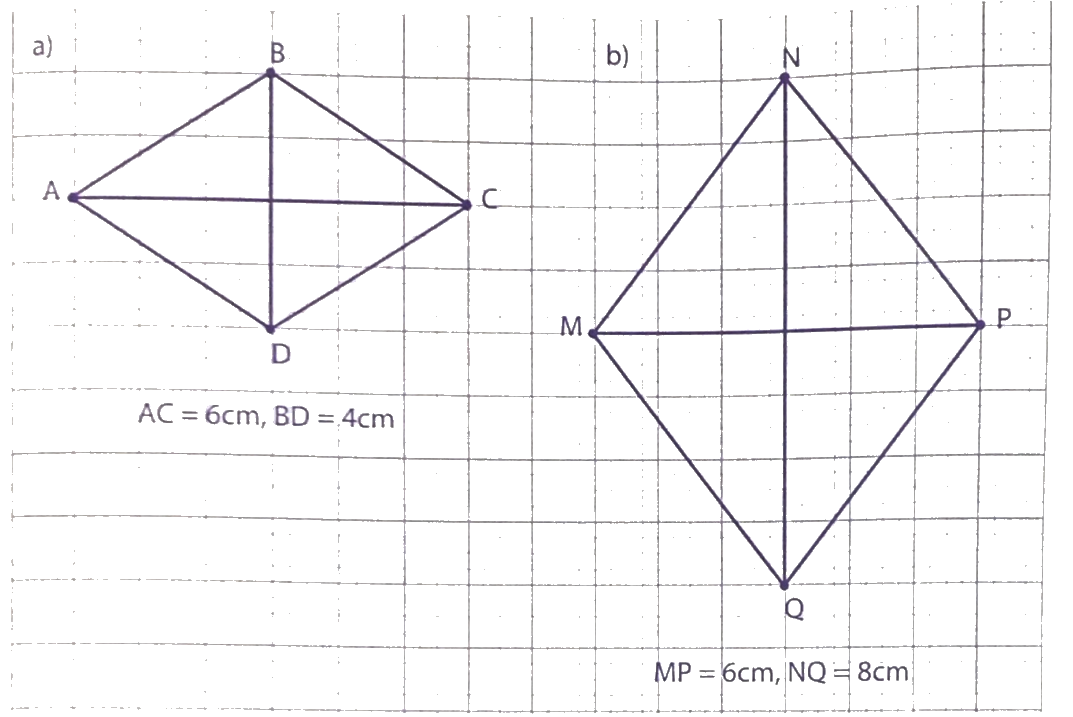
Tính diện tích mỗi hình thoi sau:
Phương pháp giải:
Để tính diện tích hình thoi ta lấytích độ dài hai đường chéo chia cho 2.
Lời giải chi tiết:
a) Diện tích hình thoi là:
$\frac{{6 \times 4}}{2} = 12$(cm2)
Đáp số: 12 cm2
b) Diện tích hình thoi là:
$\frac{{6 \times 8}}{2} = 24$(cm2)
Đáp số: 24 cm2
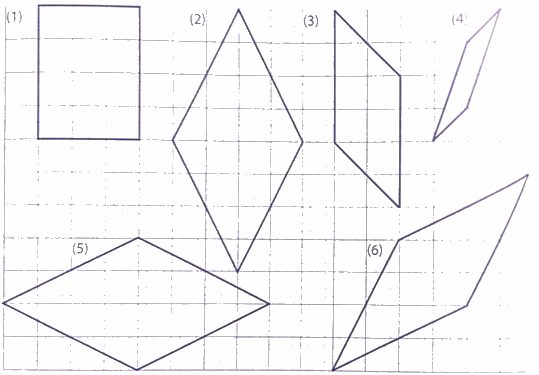
Trong các hình sau, hình nào là hình thoi?
Phương pháp giải:
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Lời giải chi tiết:
Hình (2); hình (5); hình (6) là hình thoi.
Tính:
\({\text{a) }}\frac{5}{4} \times \frac{2}{3} + \frac{1}{6}{\text{ }}\)
\({\text{b) }}\frac{{17}}{4} - \frac{2}{3}:\frac{1}{6}\)
Phương pháp giải:
Biểu thức có chứa phép cộng, phép trừ, phép nhân, phép chia thì ta thực hiện phép nhân, phép chia trước; thực hiện phép cộng, phép trừ sau.
Lời giải chi tiết:
\({\text{a) }}\frac{5}{4} \times \frac{2}{3} + \frac{1}{6} = \frac{{10}}{{12}} + \frac{1}{6} = \frac{5}{6} + \frac{1}{6} = \frac{6}{6} = 1{\text{ }}\)
\({\text{b) }}\frac{{17}}{4} - \frac{2}{3}:\frac{1}{6} = \frac{{17}}{4} - \frac{2}{3} \times \frac{6}{1} = \frac{{17}}{4} - 4 = \frac{{17}}{4} - \frac{{16}}{4} = \frac{1}{4}{\text{ }}\)
Cho các phân số: $\frac{3}{5};\frac{{32}}{{42}};\frac{{36}}{{60}};\frac{{30}}{{36}};\frac{{15}}{{24}};\frac{{16}}{{21}}.$
a) Rút gọn các phân số chưa tối giản trong các phân số trên.
b) Trong các phân số trên, những phân số bằng nhau là: .......................................................................
Phương pháp giải:
Khi rút gọn phân số có thể làm như sau:
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
a) $\frac{{32}}{{42}} = \frac{{32:2}}{{42:2}} = \frac{{16}}{{21}}$
$\frac{{36}}{{60}} = \frac{{36:12}}{{60:12}} = \frac{3}{5}$
$\frac{{30}}{{36}} = \frac{{30:6}}{{36:6}} = \frac{5}{6}$
$\frac{{15}}{{24}} = \frac{{15:3}}{{24:3}} = \frac{5}{8}$
b) Trong các phân số trên, những phân số bằng nhau là: $\frac{3}{5}$và $\frac{{36}}{{60}}$;\(\frac{{32}}{{42}}\) và $\frac{{16}}{{21}}$.
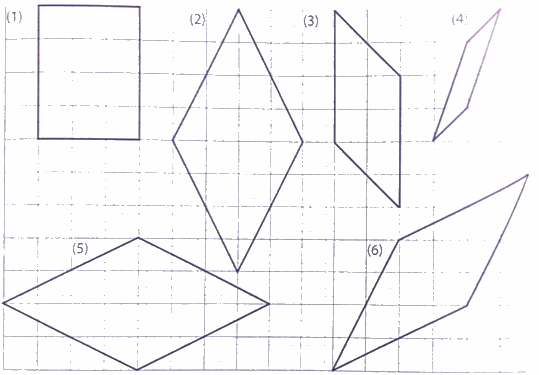
Trong các hình sau, hình nào là hình thoi?
Phương pháp giải:
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Lời giải chi tiết:
Hình (2); hình (5); hình (6) là hình thoi.
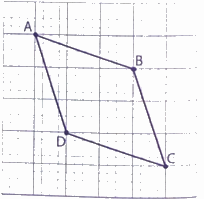
Trong hình vẽ bên, em hãy cho biết:
a) Tên các cặp cạnh đối diện.
b) - Các cặp cạnh đối diện có song song và bằng nhau không?
- Bốn cạnh có bằng nhau không?
Phương pháp giải:
Quan sát hình vẽ và trả lời câu hỏi đề bài.
Lời giải chi tiết:
a) Tên các cặp cạnh đối diện: AB và DC; AD và BC.
b) - Các cặp cạnh đối diện có song song và bằng nhau.
- Bốn cạnh có bằng nhau.
Tính diện tích mỗi hình thoi sau:
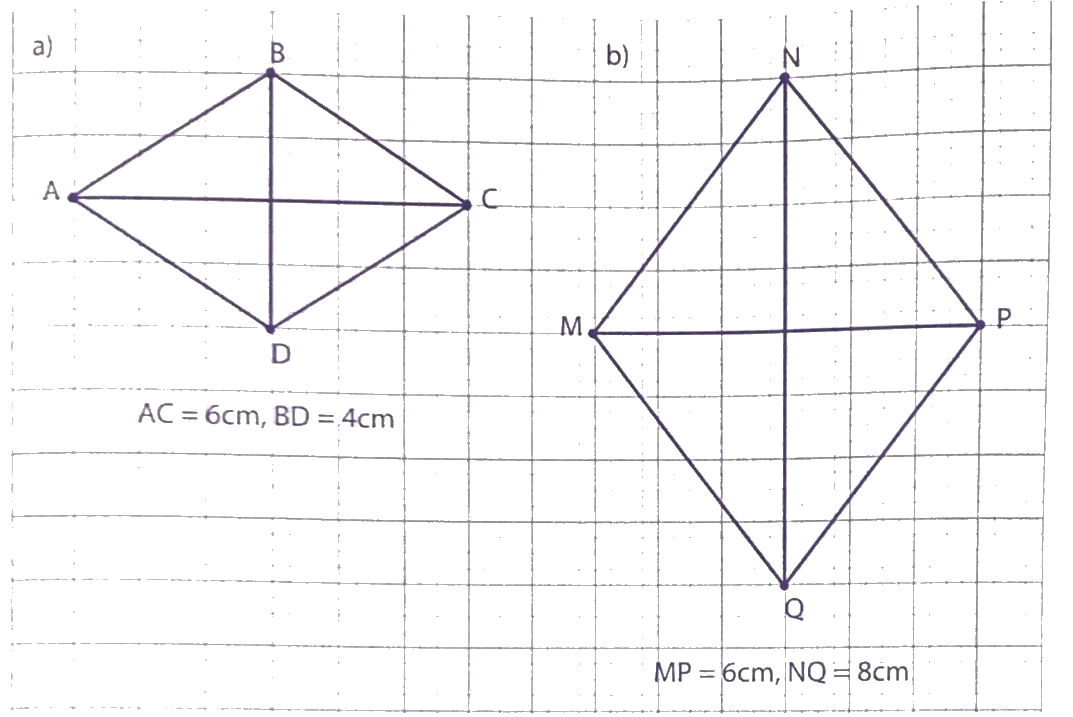
Phương pháp giải:
Để tính diện tích hình thoi ta lấytích độ dài hai đường chéo chia cho 2.
Lời giải chi tiết:
a) Diện tích hình thoi là:
$\frac{{6 \times 4}}{2} = 12$(cm2)
Đáp số: 12 cm2
b) Diện tích hình thoi là:
$\frac{{6 \times 8}}{2} = 24$(cm2)
Đáp số: 24 cm2
Bài tập phần A trong sách Toán 4 tập 2, Kết nối tri thức trang 26 tập trung vào việc ôn luyện các kiến thức về các phép tính với các số có nhiều chữ số, đặc biệt là phép cộng và phép trừ. Mục tiêu chính là giúp học sinh nắm vững các quy tắc, kỹ năng thực hiện các phép tính này một cách chính xác và nhanh chóng.
Phần A thường bao gồm các bài tập sau:
Để giải bài tập 1, học sinh cần thực hiện các bước sau:
Ví dụ: Tính 1234 + 5678
Giải:
1234 + 5678 = 6912
Để giải bài tập 2, học sinh cần thực hiện các bước sau:
Ví dụ: Một cửa hàng có 2345 kg gạo. Buổi sáng cửa hàng bán được 1234 kg gạo. Hỏi cửa hàng còn lại bao nhiêu kg gạo?
Giải:
Số gạo còn lại là: 2345 - 1234 = 1111 (kg)
Đáp số: 1111 kg
Để giải bài tập 3, học sinh cần thực hiện các bước sau:
Ví dụ: x + 1234 = 5678
Giải:
x = 5678 - 1234
x = 4444
Việc giải các bài tập phát triển năng lực không chỉ giúp học sinh củng cố kiến thức mà còn giúp các em rèn luyện tư duy logic, khả năng giải quyết vấn đề và kỹ năng tự học. Đây là những kỹ năng quan trọng không chỉ trong học tập mà còn trong cuộc sống.
Giaitoan.edu.vn luôn đồng hành cùng học sinh trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách Toán 4 tập 2, Kết nối tri thức. Hãy truy cập giaitoan.edu.vn để học toán online hiệu quả và đạt kết quả cao!
| Phép tính | Ví dụ |
|---|---|
| Phép cộng | 123 + 456 = 579 |
| Phép trừ | 789 - 123 = 666 |