Chào mừng các em học sinh đến với bài giải chi tiết phần B, trang 21 trong sách Bài tập phát triển năng lực Toán 4 tập 2. Bài viết này sẽ cung cấp cho các em những phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và đội ngũ giáo viên giàu kinh nghiệm.
Đúng ghi Đ, sai ghi S. Tính bằng hai cách:
May một chiếc túi “ba gang” hết \(\frac{4}{5}\)m vải. Hỏi may 20 chiếc túi như thế hết mấy mét vải?
Phương pháp giải:
Số mét vải để may 20 chiếc túi ta lấy số mét vải may một chiếc túi nhân với 20.
Lời giải chi tiết:
May 20 chiếc túi hết số mét vải là:
\(\frac{4}{5} \times 20 = 16(m)\)
Đáp số: 16m
Điền vào chỗ chấm cho thích hợp:
\(\frac{1}{4}\) của 36cm là: ....................................
\(\frac{1}{5}\) của 40$\ell $ là: .....................................
\(\frac{{10}}{{13}}\) của 143kg là: .................................
\(\frac{8}{{27}}\) của 216m là: ................................
Phương pháp giải:
Muốn tìm phân số của một số ta lấy số đã cho nhân với phân số đó.
Lời giải chi tiết:
\(\frac{1}{4}\) của 36cm là: $36 \times \frac{1}{4} = 9$ (cm)
\(\frac{1}{5}\) của 40$\ell $ là: $40 \times \frac{1}{5} = 8$ ($\ell $)
\(\frac{{10}}{{13}}\) của 143kg là: $143 \times \frac{{10}}{{13}} = 110$(kg)
\(\frac{8}{{27}}\) của 216m là: $216 \times \frac{8}{{27}} = 64$(m)
Một hình bình hành có diện tích \(\frac{{27}}{5}\)m2, độ dày đáy là \(\frac{9}{{10}}\)m. Tính chiều cao của hình đó.
Phương pháp giải:
Chiều cao hình bình hành = Diện tích : độ dài đáy.
Lời giải chi tiết:
Chiều cao của hình bình hành là:
\(\frac{{27}}{5}:\frac{9}{{10}} = 6\) (m)
Đáp số 6m
Đúng ghi Đ, sai ghi S:
\({\text{a) }}\frac{2}{{16}}:\frac{5}{6} = \frac{{16}}{2} \times \frac{5}{6} = \frac{{16 \times 5}}{{2 \times 6}} = \frac{{80}}{{12}} = \frac{{20}}{3}\)
\({\text{b) }}\frac{{21}}{{27}}:\frac{7}{9}{\text{ = }}\frac{{21:7}}{{27:9}}{\text{ = }}\frac{3}{3}{\text{ = 1 }}\)
\({\text{c) }}\frac{9}{{36}}:\frac{3}{4} = \frac{1}{4}:\frac{3}{4} = \frac{1}{4} \times \frac{4}{3} = \frac{{1 \times 4}}{{4 \times 3}} = \frac{1}{3}{\text{ }}\)
\({\text{d) }}\frac{{17}}{{18}}:\frac{1}{{18}} = \frac{{17:1}}{{18}} = \frac{{17}}{{18}}{\text{ }}\)
Phương pháp giải:
Kiểm tra lại cách chia hai phân số rồi xét tính đúng sai từng câu.
Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
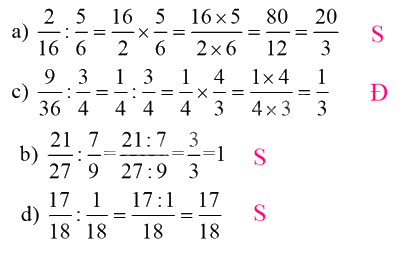
\({\text{a) }}\frac{2}{6} \times \frac{5}{9} = \frac{{2 \times 5}}{{6 \times 9}} = \frac{{10}}{{54}} = \frac{5}{{27}}\)
\({\text{b) }}\frac{2}{8} \times \frac{8}{9} = \frac{{2 \times 9}}{{8 \times 8}} = \frac{{18}}{{64}} = \frac{9}{{32}}{\text{ }}\)
\({\text{c) }}\frac{8}{{17}} \times \frac{{17}}{{24}} = \frac{{8 \times 17}}{{17 \times 24}} = \frac{8}{{24}} = \frac{1}{3}{\text{ }}\)
\({\text{d) }}\frac{9}{{16}} \times \frac{{16}}{9} = \frac{{9 \times 16}}{{16 \times 9}} = 1{\text{ }}\)
Phương pháp giải:
Kiểm tra cách nhân hai phân số để tìm ra đúng, sai của từng câu trong đề bài.
Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Lời giải chi tiết:

Tính bằng hai cách:
\({\text{a) 8}} \times \frac{6}{{32}} \times \frac{1}{5}\)
\({\text{b) }}\frac{{15}}{{16}} \times \frac{{36}}{{35}} \times 28\)
\({\text{c) }}\left( {\frac{5}{6} + \frac{{32}}{{36}}} \right) \times \frac{{18}}{{10}}\)
\({\text{d) }}\frac{9}{{16}} \times \frac{{56}}{{63}}{\text{ + }}\frac{{56}}{{63}} \times \frac{{27}}{{24}}{\text{ }}\)
Phương pháp giải:
Áp dụng tính chất:
(a x b) x c = a x (b x c).
a x (b x c) = (a x b) x c.
(a + b) x c = a x c + b x c.
Lời giải chi tiết:
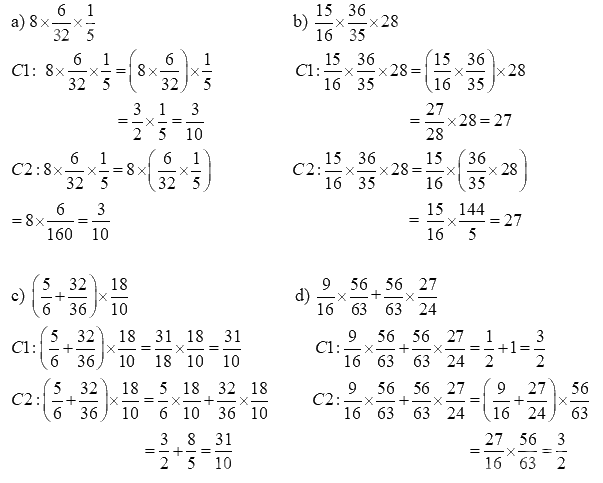
\({\text{a) }}\frac{2}{6} \times \frac{5}{9} = \frac{{2 \times 5}}{{6 \times 9}} = \frac{{10}}{{54}} = \frac{5}{{27}}\)
\({\text{b) }}\frac{2}{8} \times \frac{8}{9} = \frac{{2 \times 9}}{{8 \times 8}} = \frac{{18}}{{64}} = \frac{9}{{32}}{\text{ }}\)
\({\text{c) }}\frac{8}{{17}} \times \frac{{17}}{{24}} = \frac{{8 \times 17}}{{17 \times 24}} = \frac{8}{{24}} = \frac{1}{3}{\text{ }}\)
\({\text{d) }}\frac{9}{{16}} \times \frac{{16}}{9} = \frac{{9 \times 16}}{{16 \times 9}} = 1{\text{ }}\)
Phương pháp giải:
Kiểm tra cách nhân hai phân số để tìm ra đúng, sai của từng câu trong đề bài.
Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Lời giải chi tiết:

Tính bằng hai cách:
\({\text{a) 8}} \times \frac{6}{{32}} \times \frac{1}{5}\)
\({\text{b) }}\frac{{15}}{{16}} \times \frac{{36}}{{35}} \times 28\)
\({\text{c) }}\left( {\frac{5}{6} + \frac{{32}}{{36}}} \right) \times \frac{{18}}{{10}}\)
\({\text{d) }}\frac{9}{{16}} \times \frac{{56}}{{63}}{\text{ + }}\frac{{56}}{{63}} \times \frac{{27}}{{24}}{\text{ }}\)
Phương pháp giải:
Áp dụng tính chất:
(a x b) x c = a x (b x c).
a x (b x c) = (a x b) x c.
(a + b) x c = a x c + b x c.
Lời giải chi tiết:
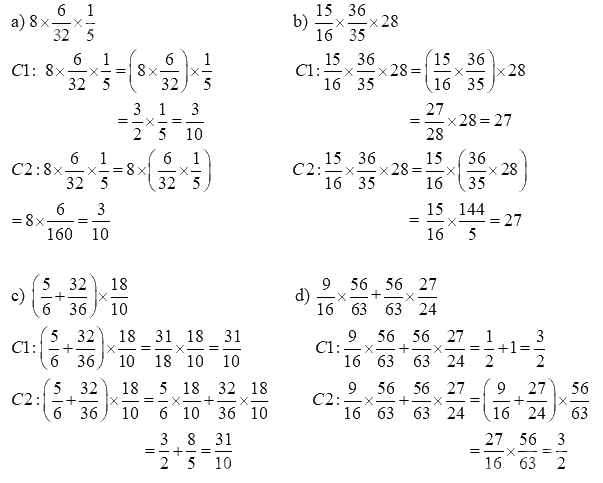
May một chiếc túi “ba gang” hết \(\frac{4}{5}\)m vải. Hỏi may 20 chiếc túi như thế hết mấy mét vải?
Phương pháp giải:
Số mét vải để may 20 chiếc túi ta lấy số mét vải may một chiếc túi nhân với 20.
Lời giải chi tiết:
May 20 chiếc túi hết số mét vải là:
\(\frac{4}{5} \times 20 = 16(m)\)
Đáp số: 16m
Điền vào chỗ chấm cho thích hợp:
\(\frac{1}{4}\) của 36cm là: ....................................
\(\frac{1}{5}\) của 40$\ell $ là: .....................................
\(\frac{{10}}{{13}}\) của 143kg là: .................................
\(\frac{8}{{27}}\) của 216m là: ................................
Phương pháp giải:
Muốn tìm phân số của một số ta lấy số đã cho nhân với phân số đó.
Lời giải chi tiết:
\(\frac{1}{4}\) của 36cm là: $36 \times \frac{1}{4} = 9$ (cm)
\(\frac{1}{5}\) của 40$\ell $ là: $40 \times \frac{1}{5} = 8$ ($\ell $)
\(\frac{{10}}{{13}}\) của 143kg là: $143 \times \frac{{10}}{{13}} = 110$(kg)
\(\frac{8}{{27}}\) của 216m là: $216 \times \frac{8}{{27}} = 64$(m)
Đúng ghi Đ, sai ghi S:
\({\text{a) }}\frac{2}{{16}}:\frac{5}{6} = \frac{{16}}{2} \times \frac{5}{6} = \frac{{16 \times 5}}{{2 \times 6}} = \frac{{80}}{{12}} = \frac{{20}}{3}\)
\({\text{b) }}\frac{{21}}{{27}}:\frac{7}{9}{\text{ = }}\frac{{21:7}}{{27:9}}{\text{ = }}\frac{3}{3}{\text{ = 1 }}\)
\({\text{c) }}\frac{9}{{36}}:\frac{3}{4} = \frac{1}{4}:\frac{3}{4} = \frac{1}{4} \times \frac{4}{3} = \frac{{1 \times 4}}{{4 \times 3}} = \frac{1}{3}{\text{ }}\)
\({\text{d) }}\frac{{17}}{{18}}:\frac{1}{{18}} = \frac{{17:1}}{{18}} = \frac{{17}}{{18}}{\text{ }}\)
Phương pháp giải:
Kiểm tra lại cách chia hai phân số rồi xét tính đúng sai từng câu.
Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.
Lời giải chi tiết:
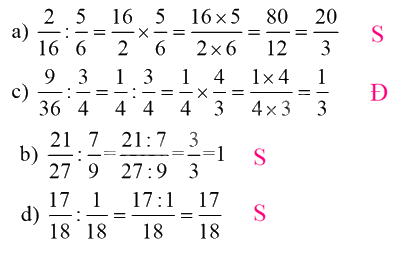
Một hình bình hành có diện tích \(\frac{{27}}{5}\)m2, độ dày đáy là \(\frac{9}{{10}}\)m. Tính chiều cao của hình đó.
Phương pháp giải:
Chiều cao hình bình hành = Diện tích : độ dài đáy.
Lời giải chi tiết:
Chiều cao của hình bình hành là:
\(\frac{{27}}{5}:\frac{9}{{10}} = 6\) (m)
Đáp số 6m
Phần B của bài tập phát triển năng lực Toán 4 tập 2, trang 21, tập trung vào việc củng cố và mở rộng kiến thức về các phép tính với số tự nhiên, đặc biệt là phép nhân và phép chia. Các bài tập trong phần này thường có tính ứng dụng cao, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề thực tế.
Phần B bao gồm một số bài tập với các dạng khác nhau. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh thực hiện các phép tính nhân và chia một cách nhanh chóng và chính xác. Để làm tốt bài tập này, học sinh cần nắm vững bảng nhân, bảng chia và luyện tập thường xuyên.
Bài tập này yêu cầu học sinh đọc kỹ đề bài, xác định đúng các yếu tố quan trọng (đề bài cho gì, hỏi gì) và lựa chọn phép tính phù hợp để giải bài toán. Việc vẽ sơ đồ có thể giúp học sinh hình dung rõ hơn về bài toán và tìm ra lời giải.
Ví dụ:
Một cửa hàng có 5 thùng kẹo, mỗi thùng có 15 gói kẹo. Hỏi cửa hàng có tất cả bao nhiêu gói kẹo?
Lời giải:
Số gói kẹo cửa hàng có là: 5 x 15 = 75 (gói)
Đáp số: 75 gói kẹo
Bài tập này yêu cầu học sinh tìm giá trị của x trong một phương trình đơn giản. Để giải bài tập này, học sinh cần hiểu rõ các quy tắc về phép toán và sử dụng các phép toán ngược để tìm ra giá trị của x.
Ví dụ: x + 12 = 25
Lời giải:
x = 25 - 12
x = 13
Kiến thức về các phép tính với số tự nhiên được ứng dụng rộng rãi trong cuộc sống hàng ngày. Ví dụ, khi đi mua sắm, chúng ta cần tính toán số tiền phải trả. Khi nấu ăn, chúng ta cần đo lường lượng nguyên liệu cần thiết. Việc nắm vững kiến thức này sẽ giúp chúng ta tự tin hơn trong các hoạt động hàng ngày.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em có thể làm thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online. Giaitoan.edu.vn cung cấp một kho bài tập phong phú và đa dạng, giúp các em học toán một cách hiệu quả và thú vị.
Hy vọng rằng bài giải chi tiết phần B, trang 21 Bài tập phát triển năng lực Toán 4 tập 2 này sẽ giúp các em hiểu rõ hơn về các kiến thức và kỹ năng cần thiết để giải các bài tập toán. Chúc các em học tập tốt và đạt kết quả cao!
| Bài tập | Mức độ khó | Lời khuyên |
|---|---|---|
| Bài 1 | Dễ | Luyện tập bảng nhân, bảng chia |
| Bài 2 | Trung bình | Đọc kỹ đề, vẽ sơ đồ |
| Bài 3 | Trung bình | Hiểu rõ quy tắc phép toán |
| Chúc các em học tốt! | ||